
| |Approximations| | |Hydrostatic| | |Geostrophic| | |Inertial| | |Shallow Water Equations| |

| |Approximations| | |Hydrostatic| | |Geostrophic| | |Inertial| | |Shallow Water Equations| |
Operational numerical models of ocean circulation, which strive for as realistic a simulation of the ocean as possible, use a complicated set of equations called the primitive equations. These describe the relationships among the variables velocity (both horizontal and vertical), density (as a function of temperature, salinity, and pressure), temperature, salinity, and pressure (due both to variations in the sea level and the internal density field) in an Eulerian framework (that is, at fixed points in space as opposed to following particles moving with the fluid). Since it takes a tremendous amount of computer power and time to solve the full set of equations, a number of different approximations are often used to simplify the equations to make them quicker and easier to solve. The trick is in knowing when it is okay to make which approximations. It depends on the regions and processes you are most interested in simulating. It should be noted that the primitive equations themselves already make some assumptions, including that the water is incompressible and Boussinesq (meaning that variations in density are considered too small to affect inertia but are important in terms of affecting buoyancy), and therefore these equations can not represent sound traveling through the water; and turbulence effects are parameterized in terms of the mean flow.
The hydrostatic approximation is a simplification of the equation governing the vertical component of velocity. It simply says that the pressure at any point in the ocean (atmosphere) is due to the weight of the water (air) above it. When vertical accelerations are small compared to the gravitational acceleration, the hydrostatic approximation is valid. Global atmospheric models, such as NOGAPS, are hydrostatic, while regional mesoscale models, such as COAMPS™, are not hydrostatic. Presently, most ocean circulation models, including all the Navy operational ones, are hydrostatic (Haidvogel and Beckmann, 2000). Non-hydrostatic ocean models are under development and are being used in research applications. The use of non-hydrostatic models is important in simulating highly convective flows and may be important in getting the details right for flows associated with high frequency internal waves, for example.
If the density were constant with depth, the hydrostatic pressure, p, in the ocean would simply be given by the product of the gravitational acceleration, g, the depth, z (taken to be positive downward in the equation below), and the density, 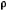 .
.
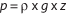
However, since density varies with depth, the pressure at any point equals gravity times the integral of density from the surface down to the depth in question.
The geostrophic approximation is a simplification of the equations governing the horizontal components of velocity. It is valid when the largest terms in the equations of motion are those involving the Coriolis force and the pressure gradient. This is generally true in the deep ocean over large (> 100 km) spatial and long (>2 days) temporal scales. Geostrophic flow represents a steady-state balance (i.e. there is no variation in time) between the pressure gradient and Coriolis forces.
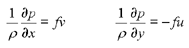
The inertial frequency, f, is the component of the earth's rotation perpendicular to the ocean surface.
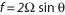 , where
, where 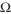 is the earth's rotation rate and
is the earth's rotation rate and 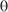 is the latitude (positive in the northern hemisphere and negative in the southern).
Note that f goes to 0 at the equator.
is the latitude (positive in the northern hemisphere and negative in the southern).
Note that f goes to 0 at the equator.
Unlike in the atmosphere, it is not possible to reliably make measurements of pressure at level surfaces in the ocean. Traditionally in the ocean, the pressure gradient term has been arrived at by integrating the specific volume between two pressure surfaces, often a deep reference pressure and the sea surface, to get the dynamic height at a number of locations.
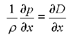
It is often true that the horizontal pressure gradient, and hence the geostrophic velocity, decreases with depth in the ocean. This has led to the choice of a reference level, called the level of no motion, at which it is assumed that there is no horizontal pressure gradient and no geostrophic velocity. It also means that pressure gradients due to slopes in the sea surface (and we're talking about large-scale slopes here, not those due to surface gravity waves) are compensated for, and reduced by, the subsurface density field. This can only happen if the density surfaces slope oppositely to the sea surface.
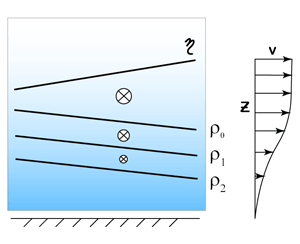
This allows us to infer the direction of sea surface slope from the slope of isopycnals (lines of constant density). The following schematic depicts a northern hemisphere warm core eddy, with the upper part of the figure showing the circulation of the eddy as clockwise from above, and the lower part of the figure showing that the sea surface is higher, as viewed from the side.
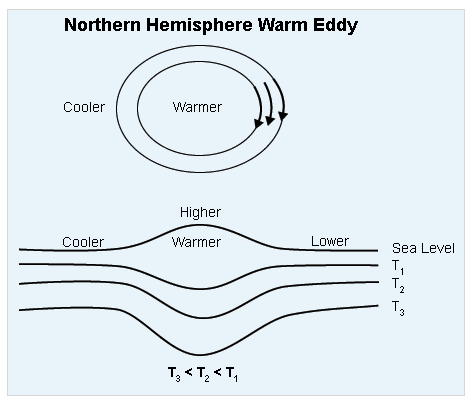
As in the atmosphere, water flows to the right when facing from high to low pressure, in the northern hemisphere. In the northern hemisphere, the warmer (or less dense) water is on the right when facing the direction towards which the current is flowing, as is illustrated in the following image.
In reality, there may be non-zero velocity at the reference level, so geostrophic velocities calculated in this way are not absolute velocities, but rather are relative to the reference level. Thus, we may refer to the geostrophic shear, also called the thermal wind, since the atmospheric analog is that horizontal variation in temperature causes vertical variations in the wind. This method was used because the most abundant measurements in the ocean were of temperature and salinity, which allowed for calculation of the density, or specific volume.
The absolute geostrophic velocity can be estimated if the actual slope of any pressure surface is known, or if the geostrophic velocity at any pressure level is known. Today, it is possible to determine the absolute geostrophic velocity by measuring the slope of the sea surface remotely by satellite altimetry and integrating the dynamic height relative to it, or by measuring the velocity at the reference pressure where frictional influences and temporal variability are thought to be small and adding it to the velocity at all other levels.
While large-scale currents in the deep ocean, such as the Gulf Stream and Kuroshio, and even many currents in coastal regions, such as coastal upwelling jets, are largely geostrophic, it can be more problematic applying geostrophy in shallower water. Even besides the inherent problems that the short time scales and importance of bottom friction may render the basic assumption of geostrophy invalid, there are technical issues in how to calculate the geostrophic current near shore where the water depth is less than the reference level. Unfortunately, use of remotely sensed sea level may not offer relief to this dilemma since the accuracy of these data is degraded near the coast. It should also be noted that the geostrophic approximation breaks down near the equator where f goes to zero.
Inertial motion is a balance between the local acceleration (time derivative of velocity)
and the Coriolis forces.
The signature of inertial motion is a circular trajectory that repeats with
a period of 2 /f, or 12 hours divided by the sine
of the latitude.
/f, or 12 hours divided by the sine
of the latitude.
The shallow water equations, also known as the LaPlace tidal equations, make several assumptions to simplify the full set of primitive equations. They assume the fluid is hydrostatic. More significantly, the assumption is made that the fluid is homogeneous, i.e. there are no variations in density. Therefore there is no baroclinic pressure gradient or velocity. They may also assume the nonlinear and friction terms are small, thus rendering the equations linear (i.e. advection terms for velocity are ignored) and inviscid.
Continue on to the last section of this module: Surface and Bottom Boundary Layers