Today's ice concentration (for a model grid element for instance) is a function of yesterday's (for a 1-day time step) concentration modified by physical processes that change the concentration. The processes are advection of ice area into or out of the element, deformation within an element, melt of ice area (top and bottom melt of thin ice and lateral melt of ice too thick to melt through during one time step) and growth of open water into new ice area. The ice model calculates these changes. The changes in concentration for each grid element is only weakly related to concentrations for distant grid elements; it takes time for concentration information to be transmitted through the ice model. During each time step at most 4 other elements exchange ice with any one element.

Linear Kalman filtering (discreet time) is one data assimilation technique suited to this kind of problem. Details of Kalman filtering can be found in many texts [e.g., Gelb, Applied Optimal Estimation , MIT Press, 1986].

The elements of Kalman filtering consists of a physical model, M, that propagates the state variables, X, (just ice concentration in this instance) and the estimation error covariance forward in time, a gain, K, that weights new observations based on the estimation error and observation error variances, and an observation model, H, that relates the state, to the observations, Z (i.e., Z =HX). The gain is chosen so as to minimize the estimation error variance.

The predicted X at time step k is given by

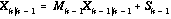  (1)

where the k|k-1 subscript indicates a value at time step k with data assimilated up to time step k-1. 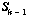is an inhomogeneous source term arising when two state equations (one for the concentration of open water, one for the concentration of ice) are reduced to one (open water concentration is just 1-ice concentration). 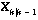is the modeled concentration at time step k starting from the filtered solution at k-1. The assimilation step is

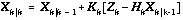(2)

where 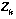is the new observation and 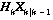is the predicted state transformed into measurement space by the observation model.

The observation model can be the "forward model" for satellite passive microwave observations as discussed by Maslanik; given the concentration of ice and open water, plus values for several other variables/parameters, the observation model gives an estimate of brightness temperature as observed by the satellite. While this may be the most elegant way to handle the satellite observations, I decided ~10 years ago that there were too many unknown variables/parameters in the radiative transfer equation that needed to be estimated, perhaps using estimated mean values, and too much tweaking needing to be done so that the estimated brightness temperatures agreed with observations, that one might as well use an algorithm estimate of concentration. (In which case the observation model is just the identity operator.) This situation may have changed, or will change, so the "forward model" should be considered. In addition, there may be other, simultaneous, observations of ice concentration besides the satellite passive microwave that can be assimilated by using a different observation model. Independent but simultaneous observations can be handled in Kalman filtering by considering them to occur serially over a zero (i.e., very short) time span.

The physical model is, in theory, just the ice model itself. Since the model is nonlinear, a linearized approximation is necessary. My solution has been to write the model as a linear function involving rates of change of ice area due to advection and to thermodynamics. The rates are just those necessary to explain the changes produced by the full ice model. This "piece-wise linear" area model simply tracks the ice model.

A problem with this technique is deciding how to change the model solution when assimilating concentration data. If the filtered concentration estimate shows more ice in a model grid element than the model alone estimates, what changes should be made to the modeled ice thickness distribution? If the too low model estimate is due to too little import of ice from an adjacent cell, then one should increase the import of ice from that cell, with the imported ice having the donor cell's thickness distribution. If the model estimate is too low due to too much export, then less ice with the current thickness distribution should be exported. The too low model estimate might also be due to too little ice growth or too much ice melt. If melting, how much of the area melt is due to melt of the thinnest ice and how much due to lateral melt of ice of all thicknesses? In general, the problem is underdetermined; there are more model processes (cell-to-cell area advections, growth or melt rates) than equations (one concentration equation for each cell). One must either go to a more complex assimilation scheme, make some assumptions about which processes to change, or choose some ad hoc method for adding or removing ice (e.g., scaling the ice thickness distribution for thickness>0 to fit the Kalman filter concentration estimate).

The Kalman filter involves solving a matrix equation where the matrices have dimension equal to the number of grid elements times the number of state variables (which is just one for ice concentration). For grids with hundreds of grid elements, solving the equation involves multiplication and inverses of large matrices. I assume that during a time step each grid element interacts with just the adjacent grid elements (at most 4) and that assimilation for each element is independent of the assimilation in other element. Then the computations amount to hundreds (number of grid elements) of matrix equations, each of dimension 5 (5 elements times 1 state variable). These are easily solved.

Assimilating Velocity Data

One could use a Kalman filter to assimilate ice velocity observations into the ice model, but there are problems with a strictly temporal approach. First, some kind of spatial interpolation would still be necessary to go from the velocity at a Lagrangian point to velocities on a fixed grid. Second, if the model velocity differed much from the observed velocity and if velocity observations were sparse, one would have small regions (on the order of a model grid element) about the observations moving differently from the surrounding ice, resulting in bands of intense ice deformation about each observation.

Another way to assimilate velocities is to make use of the spatial autocorrelation of ice velocity, as in Thorndike [in The Geophysics of Sea Ice, Plenum Press, N.Y., 1986]. I have used optimal interpolation to assimilate buoy velocities into an ice model. While this gives more realistic looking velocity fields, it does not eliminate the spurious deformations caused by systematic errors in the modeled velocities, but spreads them out over scales on the order of 800 km. The array of buoys (~500 km apart) reduces the spurious deformation but does not eliminate it.

The optimal interpolation procedure is summarized by

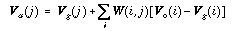  (3)

where 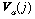is the assimilation estimate at location j, 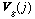is the initial guess or background at j, 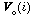is the observed value at i, 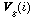is the guess at i, and 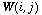are the weights to give each observation. See Thorndike [1986] for determining the weights. For the initial guess one can use the long term mean velocity field as determined from buoy observations. The individual buoy velocities are observations to assimilate into the first guess, and the modeled velocities are treated as another kind of observation. Justification for doing this is that due to measurement errors in buoy velocities, separation of the observation from the interpolation point, and modeling errors, we do not have complete information about the velocity at any point. The lack of information is reflected in the shift of the interpolated velocity toward the mean. A problem with doing this is that we do not have a good estimate of the mean velocity field. In some areas there are no buoy data at all; where there are data, there are varying number of observations. One solution is to start with no information (velocity field zero everywhere) and use optimal interpolation to assimilate the sample mean velocities (with "observation error" standard deviation equal to the standard error of the mean at that location). The buoy velocities are binned into the model grid, and averaged to give the sample mean field.

Another view is to consider the modeled velocity field as the initial guess and interpolate the observations into this field. This give a slightly different velocity field than when using the mean as the initial guess.

Does optimal interpolation smooth the velocity field? If it does, the ice deformation will be too small. One assumption is that observed velocities include measurement errors with zero mean and known variance. Eliminating velocity variations due to errors seems desirable although for each individual observation we have no way of knowing what the error is. The interpolated field will be smoother than the raw velocity data but this kind of smoothing is good.

However, if the true velocity field contains variations on spatial scales not sampled by the observations (which is likely the case for historical buoy data), then the model/assimilated velocity field will underestimate the deformation. And if the modeled velocity field does not contain enough spatial variability, the deformation will also be underestimated. This seems to be the case for an ice model that uses spatially constant drag coefficients. So assimilating sparse velocity data into a too smooth model velocity field will tend to underestimate deformations.

Systematic errors in the modeled velocity field is probably the most important problem to address. One way to avoid the problem is to use observed velocities everywhere. The only present source for such observations are those from satellite passive microwave images, generally in the form of displacements over several days (see below for assimilating displacements). Multiday ice motions would be heavily influenced by the data, with temporal variability provided by the modeled velocities. This will reduce the spurious deformation caused by incompatibilities between observed and modeled velocities. More realistic spatially and temporally varying air and water drag coefficients for the model will also improve estimates of deformation. Perhaps the 10 km resolution of the PIPS 3 model will itself increase spatial variability in ice velocity. As a last resort, one could simply add a sub-grid scale source of deformation.

Assimilating Other Data

I have concentrated on assimilating buoy velocities and SSMI derived ice concentration into a model, but other data are, or will become, available. One data source is displacement fields derived from satellite images (e.g., SSMI and SAR). Assuming that the displacements occur over multiple model time steps, how can they be assimilated into the model?

The straightforward method involves modeling the displacement period twice. The first pass would be without assimilating the displacement data (but other data could be assimilated). The modeled trajectory (starting from the location where the observed displacement begins) over the same period as the observation could then be scaled and rotated to match the observations. The scaled velocities for each time step would then be used as "observations" for assimilating into a second model run. The details missing from this description are how to treat start and end times for an observation if they are not at the beginning of a model time step, and what the error variance is for the resulting "observations".

Another likely data source is concentration of thin ice derived from SAR images. This can easily be handled in the Kalman filter procedure. Instead of one state variable, total ice concentration. there would be two, thin ice concentration and "other" ice concentration. SAR derived estimates of multiyear ice concentration could also be handled if the model has a separate multiyear ice thickness distribution.

Another set of data is the deformations estimated from pairs of SAR images of the same area. One way to treat these data is to assimilate them into the modeled deformations. Another way is to consider them as a set of displacements and treat them as suggested above.

Data Assimilation into a Forecast Model

Assume the model can be run in two modes; a forecast mode and an assimilation mode. The only difference may be that no data is assimilated in the forecast mode. The assimilation mode is run from previous "last data" (at Now-k days, say) to present "last data" (at Now-m days). This last result is used as initial conditions for the forecast model, which then runs from "last data" to present(Now), if necessary, then continues for the forecast period (Now+n days, say). This means that the model must simulate each day k+n times. All this also applies to the data that forces the ice model--the weather. That is, driving the model with observed weather then switching to forecast weather after the last weather analysis.

Additional model simulations may be required if the assimilation data are available at different time lags. Suppose, for instance, that the ice concentration data is available at a one day lag and ice velocity data lags 3 days. It would then be desirable to run the model in two assimilation modes. One calculation would assimilate both concentration and velocity, stopping 3 days in the past. The second calculation would start from there (3 days ago) and assimilate just concentration for the next two days. This 1 day old result would then be the initial conditions for the forecast model. Displacement data may also require an additional model simulation as mentioned above. Depending on data availability, the optimal sequence of data assimilation and forecasting could require 9 or 10 repetitions of the model. Since 6 repetitions are needed for making daily 5-day forecasts (redo previous day using observed weather, then 5 forecasts), data assimilation increases the computer processing time by about 50%.

As a by-product, the final assimilation model results give a time history of the ice properties, based on the model and the assimilated data. This record is not the best analysis possible since each analysis uses only past data. A smoothing (as opposed to filtering) technique enables use of all the data, including that taken after the analysis time. Smoothing will not affect forecasting however, since the assimilated results at the "last data" time already contain the effect of all the data.