Peter J. Stein
Scientific Solutions, Inc.
James K. Lewis
Ocean Physics Research & Development
1. INTRODUCTION
Thermal forcing can result in relatively large stresses within a floe, and ensuing tensile stresses can result in fracturing. This fracturing leads to noise within the water column, with greatest intensities at the range of about 500-1500 Hz. However, the stress state at a specific location within the floe is a complex function of the stress state time history plus the existing stresses throughout the rest of the floe. As a result, predicting under-ice noise variations due to thermal forcing has been a difficult task.
Here, we combine two theories which provide for an enhanced capability to predict under-ice noise resulting from thermally-induced fracturing. The first theory deals with the thermo-mechanics of pack ice. This theory is detailed in Lewis (1998) and provides a means of relating stresses in floes to thermally-induced strain rates. The second theory deals with the propagation of energy through the ice-ocean regime. The energy results from the fracturing of the ice (as determined from the thermo-mechanics), and each fracture is assumed to be a monopole source. The basics of the propagation theory are based on the governing equations for compressional and shear waves in ice and compressional waves in water (Stein, 1986). This can be used to determine the loss of energy with range and depth for any given frequency. This provides a means of calculating transmission loss versus range for a fracture occurring at any depth within a floe. Two simplifying assumptions are made, the first being that any two fractures do not overlap in time and the second being that the fractures are evenly distributed in space. This allows us to integrate the transmission loss curves to generate curves of relative noise levels at a given depth under the ice for fracturing at any given depth with a floe. Thus, we have a means of calculating the mean noise level within the water column for fractures occurring over a given time period.
These theories provide a means of making some general seismoacoustic predictions based on the time and location of an individual fracturing event in a floe and the propagation of the resulting energy through the ice-water media. Numerical simulations using the thermo-mechanics provide a time history of the number of fractures per time step as well as the location of the fracture relative to the surface of the ice.
Under-Ice Noise Model
The under-ice noise model is based on the propagation of energy through the ice and into the water column. The energy source is a fracture in the ice which is assumed to be a simple, compact volume expansion in the ice (a monopole source, with the radiated field independent of angle). We use the governing equations for compressional and shear waves in ice and compressional waves in water (Helmholtz equations). The ice and water column are divided into n levels in the vertical, with each level having its own compressional and shear wave speeds. Solutions in each level are assumed to be of the form which allows horizontally and vertically propagating waves (Stein, 1986).
The propagation of the energy from a fracture is modeled using the above expressions assuming that compressional stresses, shearing stresses, and vertical velocities are continuous at the interface between any two adjacent levels. It is also assumed that the stresses at the air/ice interface are zero and that shearing stresses at the ice/water interface are zero. The ice has a uniform thickness with properties which are independent of horizontal direction. The bottom of the ocean is also considered, such as a layer of silt sediment over a sand sub-bottom with elastic properties as specified in Schmidt (1988).
Within the water column, the sound speed profile can be determined from an ocean model such as that being used in PIPS 2.0. To obtain realistic wave speeds within the ice, we estimate the Young's modulus using a modification of the effective elastic modulus as determined in the thermal stress model. But the vertical distribution of E' for thermal stressing is based on very small strain rates (~10-5/s). The strain rates for fracturing events are considerably higher (order of the frequency of interest), so an adjustment must be made to obtain Y from a corresponding E'. Mellor (1986) presents data showing the dependency of elastic modulus versus frequency. From these data, it was determined that a uniform 3 GPa should be added to E' to estimate Y.
The system of wave equations for each vertical level is solved using the seismo-acoustic, fast field algorithm discussed by Schmidt (1988). A simulation is made for a source at a certain depth in the column of ice, and we assume that every source has the same strength. Simulations at a given frequency are made by varying the source from the surface of the ice to the ice-water interface over the entire thickness of the ice. These simulations are performed for a variety of snow covers on the ice to assess the impact of the insulation of the snow on the estimated value of Y and, thus, the propagation of the fracturing energy. Each simulation provides pressure (determined from particle velocity, sound speed, and water density) resulting from a fracture in a unit area of ice cover for any given distance beneath the ice at any given horizontal distance away from the fracture in the ice.
We utilize these pressure versus range curves by assuming that all fractures over a given time interval DT do not interact with one another. We then assume that the predicted fractures within a given layer of the ice are uniformly distributed over the ice layer in the horizontal direction. These assumptions allow us to integrate the pressure per unit area at a given depth in the water column z over range to get a relative noise intensity:
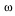 ) =
) = 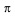 (
( t/
t/ T)
T) 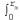 < p2 > r dr
< p2 > r dr
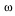 ) is our calculated pressure at a specific depth z beneath the ice, the angle brackets
indicate time averaging, r is the range variable, and rm is the range beyond which fractures contribute little if any to
the intensity of the under-ice noise.
) is our calculated pressure at a specific depth z beneath the ice, the angle brackets
indicate time averaging, r is the range variable, and rm is the range beyond which fractures contribute little if any to
the intensity of the under-ice noise.
Under these assumptions, we can calculate I for any given depth below the ice for any given frequency. This
can be done for any given snow cover. This provides us with relative levels of under-ice noise for the fractures at
different depths within the ice.
3. DISCUSSION
We have combined the thermo-mechanics of pack ice with seismo-acoustic propagation theory to provide a means of relating under-ice noise to thermally-induced fracturing in floes that are typical of the pack. The predicted stresses and fracture events are those we would expect to find within a typical floe. Thus, we are talking about floes of the order of 3-5 km in diameter and 1.5 to 2 m thick. The inputs to the numerical simulations are the thermal forcing at the surface and bottom of a floe and an estimate of the flaw structure. The acoustic propagation theory provides the connection between the predicted fracture counts and the under-ice noise. The theory allows us to calculate propagation loss as a function of where the fracture occurred with the floe.
By making the assumption that the fractures are evenly distributed in space, we can use the transmission loss curves for various times and various snow covers to generate noise intensity curves I. We see that variations in season and snow cover can result in differing noise intensity curves. The impact of snow cover is the most significant in the lower parts of a floe during the more winter-time conditions. We also see that the contributions to the overall noise levels reach a limit at a range of ~100 km.
Overall, the combination of the thermo-mechanics and acoustic propagation theory provides a means of
explaining and modeling the variability of thermally-induced, under-ice noise.
REFERENCES
Lewis, J. K., 1998: The thermo-mechanics of pack ice. In press, J. Geophys. Res.
Mellor, M., 1986: Mechanical behavior of sea ice. In The Geophysics of Sea Ice (N. Untersteiner, ed.). Plenum Press, New York, 165-281.
Schmidt, H., 1988: Seismo-acoustic fast field algorithm for range-independent environments - user's guide. Supreme Allied Commander, Atlantic, Under-Sea Res. Cnt., Rpt. SR-113, 152 pp.
Stein, P. J., 1986: Acoustic monopole in a floating ice plate. Ph.D. Disser., Mass. Inst. Tech. 315 pp.