Miles G. McPhee
Parameterization depends very much on the complexity of the ocean model:
 (1)
(1)
where
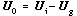 is vector ice velocity relative to undisturbed geostrophic ocean currents,
is vector ice velocity relative to undisturbed geostrophic ocean currents, 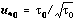 is vector friction velocity (square root of the kinematic stress, in the same direction); and
is vector friction velocity (square root of the kinematic stress, in the same direction); and 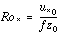 is the surface friction Rossby number;
is the surface friction Rossby number; 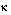 is von Karman's constant (0.4) and A and B are Rossby similarity constants, each equal to about 2.
is von Karman's constant (0.4) and A and B are Rossby similarity constants, each equal to about 2.
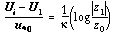 where
where 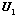 and
and 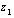 refer to the velocity and elevation of the first model gridpoint. Note that
refer to the velocity and elevation of the first model gridpoint. Note that 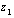 refers to a reference depth in the fluid-- not ice thickness.
refers to a reference depth in the fluid-- not ice thickness.
McPhee, M. G., 1998. Parameterization of mixing in the ocean boundary layer, in press: J. Fluid Systems.
McPhee, M. G., C. Kottmeier, J. H. Morison, 1998. Ocean heat flux in the central Weddell Sea during winter, in press: J. Phys. Oceanogr.
Both available in Adobe pdf format by anonymous FTP. Login as anonymous to nansen.apl.washington.edu; cd anzflux/mcphee; binary; get JFS98.pdf, JPO98.pdf.
2. Heat and Salt Flux at the Ice/Ocean Interface
Principles (sometimes overlooked):
- Ice can grow when the mixed layer is above freezing-- if it didn't the Weddell Sea would have no sea ice.
- Heat transfer between the ocean and the ice depends on both the elevation of mixed layer temperature above freezing and the friction velocity (
- An unexpected result of turbulent heat flux measurement programs in recent years is that the turbulent Stanton number (heat transfer coefficient) shows little dependence on the undersurface roughness (
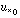 ) at the ice/ocean interface.
) at the ice/ocean interface.
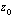 ). This runs counter to expectations from laboratory studies of heat and mass transfer across hydraulically rough surfaces, but much simplifies parameterization:
). This runs counter to expectations from laboratory studies of heat and mass transfer across hydraulically rough surfaces, but much simplifies parameterization:
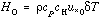 (2)
(2)
for
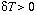 where
where 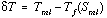 is the elevation of mixed layer temperature above freezing;
is the elevation of mixed layer temperature above freezing; 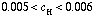 is the observed range for the exchange coefficient (turbulent Stanton number. This provides the upper boundary condition for the heat conservation equation:
is the observed range for the exchange coefficient (turbulent Stanton number. This provides the upper boundary condition for the heat conservation equation:
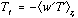 + horizontal diffusion + advection (3)
+ horizontal diffusion + advection (3)
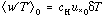
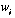 . The basal melt or freeze rate may be similarly expressed as a vertical interface velocity,
. The basal melt or freeze rate may be similarly expressed as a vertical interface velocity, 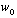 , which depends on the ocean heat flux (
, which depends on the ocean heat flux (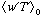 ) and heat flux conducted away from the interface in the ice cover:
) and heat flux conducted away from the interface in the ice cover: 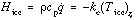 where
where 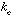 is ice thermal conductivity. To a fair approximation the salinity flux may be expressed as
is ice thermal conductivity. To a fair approximation the salinity flux may be expressed as 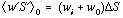 where
where 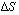 is the difference between mixed layer and ice salinities. Substituting, the salinity flux boundary condition is:
is the difference between mixed layer and ice salinities. Substituting, the salinity flux boundary condition is:
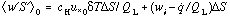 (4)
(4)
where
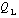 is latent heat of fusion (adjusted for brine volume) divided by specific heat of seawater (
is latent heat of fusion (adjusted for brine volume) divided by specific heat of seawater (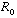 in Chang and Preller).
in Chang and Preller).
McPhee, M. G., 1992. Turbulent heat flux in the upper ocean under sea ice, J. Geophys. Res., 97, 5365-5379.