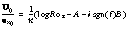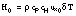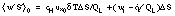Session leader: Miles McPhee
Session rapporteur: Tim Stanton
Presenters: McPhee, Stanton, Jinlun Zhang, Mike Steele, Bill Hibler
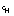 , varies little with undersurface roughness, and appears to lie in the range 0.005 <
, varies little with undersurface roughness, and appears to lie in the range 0.005 < 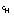 < 0.006.
< 0.006.
- Salinity flux at the interface depends on the enthalpy balance at the ice undersurface (bottom ablation/growth) as well as a "percolation" velocity representing runoff and freshwater percolation through summer ice. A specific formula for the flux boundary condition was suggested.
- Illustrated large changes in upper ocean characteristics over short drift distances observed recently during SHEBA, in the context of requiring high resolution (Rossby deformation radius) in ocean models.
- Pointed out the utility of simple (buoy) measurements of temperature, salinity, and relative current in the mixed layer for model verification and possible real time assimilation.
- Stanton:
- Expressed the need for simple but effective mixed layer formulations in a coupled ice-ocean model, including realistic treatment of fluxes of heat and salt in the upper pycnocline, illustrated by examples from SHEBA where measured oceanic heat flux exceeded 30 W m-2 in mid-winter, due to mixed-layer/pycnocline mixing.
- Stressed the requirement for an ocean model with enough vertical and horizontal resolution to adequately treat large variability in the upper pycnocline, especially important topographic effects.
- Zhang:
- Emphasized the importance of mixed layer dynamics in coupled ice-ocean models, as opposed to a constant slab upper ocean, and discussed a comparison of the approaches using models of the Arctic and GIN seas.
- Embedding a Kraus-Turner mixed layer model led to significant changes in model response, particularly in the GIN seas, and to improved predictions of ice edge position in the Greenland and Barents Seas.
- Steele:
- Discussed potential problems with restoring ocean characteristics to climatology, by showing (i) that the standard Levitus atlas has very few points in the central Arctic, especially during winter; and (ii) that model results may vary significantly depending on the restoring scheme.
- Described details of the new Environmental Working Group gridded climatology for the Arctic which includes a large amount of FSU data, and recommended that if restoring to climatology is used, then restore to EWG.
- Hibler:
- Showed that the methods for coupling most ice-ocean models severely overdamp inertial motion, and that neglect of high frequency deformation processes may miss important heat transfer and ice production mechanisms.
- Used an ice-ocean model which considers the momentum of the entire ice/mixed-layer system combined with an ice stress model to illustrate a banded offshore ice concentration structure that persists for several inertial periods after cessation of an onshore wind pulse.
- Recommendations
- Following B. Semtner's summary, recommendations are separated into immediate suggestions for the startup phase of PIPS 3.0, and then for additional improvements for longer term modeling goals. (Some of the recommendations listed below resulted from informal discussions following the meeting.)
- Immediate
- Ice/Ocean Drag
- Express ice/ocean drag (friction velocity at the ice/ocean interface) in terms of a Rossby-similarity drag law (McPhee, 1979):
- where
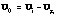 is vector ice velocity relative to undisturbed geostrophic ocean currents,
is vector ice velocity relative to undisturbed geostrophic ocean currents, 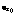 is vector friction velocity (square root of the kinematic stress at the interface, in the same direction);
is vector friction velocity (square root of the kinematic stress at the interface, in the same direction); 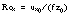 is the surface friction Rossby number;
is the surface friction Rossby number; 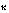 is von Kármán's constant (0.4); f is the Coriolis parameter; A and B are Rossby similarity constants, each equal to about 2; and i is the imaginary number.
is von Kármán's constant (0.4); f is the Coriolis parameter; A and B are Rossby similarity constants, each equal to about 2; and i is the imaginary number.- Rossby similarity differs from quadratic drag by allowing the effective drag coefficient and boundary layer turning to vary with ice speed. For a given ice velocity, the primary variability in (1) comes from changes in
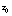 , the undersurface roughness length. Large variation (several orders of magnitude) in
, the undersurface roughness length. Large variation (several orders of magnitude) in 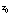 has been documented, ranging from hydraulically smooth under fast ice near Resolute Bay, to 1-2 mm in first year (seasonal) sea ice in the Weddell Sea, to as much as 10 cm in the marginal ice zone and multiyear ice packs of the Arctic. Even at a fixed location,
has been documented, ranging from hydraulically smooth under fast ice near Resolute Bay, to 1-2 mm in first year (seasonal) sea ice in the Weddell Sea, to as much as 10 cm in the marginal ice zone and multiyear ice packs of the Arctic. Even at a fixed location, 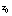 may vary depending on upstream ice conditions. Pending analysis of the extensive SHEBA data set, we recommend a three-tier classification for
may vary depending on upstream ice conditions. Pending analysis of the extensive SHEBA data set, we recommend a three-tier classification for 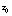 : (a) 0.05 m for multiyear ice; (b) 0.0015 m for first-year (seasonal) ice; and (c) 0.10 m for multiyear marginal ice zone regions (e.g., where ocean swell plays a role in breaking up multiyear floes). Using a typical value for U0 of 0.1 m s-1 in (1), corresponding conventional drag coefficients are 0.0053, 0.0023, and 0.0065, for multiyear, seasonal, and MIZ ice types respectively. Turning angles are 23°, 15°, and 25°. Using Rossby similarity, these values will vary with ice speed. The first is reasonably close to the value determined from the AIDJEX summer force balance (0.0055, see McPhee, 1980), often cited as the constant ocean drag coefficient in ice models. The year-long record from SHEBA should help determine a representative multiyear value, but it should be noted that we expect it to vary in multiyear ice depending on deformation history.
: (a) 0.05 m for multiyear ice; (b) 0.0015 m for first-year (seasonal) ice; and (c) 0.10 m for multiyear marginal ice zone regions (e.g., where ocean swell plays a role in breaking up multiyear floes). Using a typical value for U0 of 0.1 m s-1 in (1), corresponding conventional drag coefficients are 0.0053, 0.0023, and 0.0065, for multiyear, seasonal, and MIZ ice types respectively. Turning angles are 23°, 15°, and 25°. Using Rossby similarity, these values will vary with ice speed. The first is reasonably close to the value determined from the AIDJEX summer force balance (0.0055, see McPhee, 1980), often cited as the constant ocean drag coefficient in ice models. The year-long record from SHEBA should help determine a representative multiyear value, but it should be noted that we expect it to vary in multiyear ice depending on deformation history.- Ice/Ocean Heat Flux
- Based on several studies of oceanic heat flux under drifting sea ice (e.g., McPhee, 1992; McPhee et al., 1998), the following formula for ice/ocean heat flux is recommended for both the enthalpy balance at the ice undersurface, and as the upper boundary condition for the heat conservation equation in the ocean model:
- for
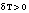 and zero otherwise, where
and zero otherwise, where 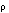 is mixed layer density;
is mixed layer density; 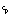 is specific heat of seawater (
is specific heat of seawater (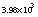 J kg-1 K-1 is representative for seawater near freezing);
J kg-1 K-1 is representative for seawater near freezing); 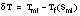 is the departure of mixed layer temperature from freezing; and
is the departure of mixed layer temperature from freezing; and 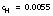 is a constant heat transfer coefficient (McPhee et al., 1998). As with
is a constant heat transfer coefficient (McPhee et al., 1998). As with 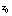 , SHEBA analysis may help refine the estimated value for
, SHEBA analysis may help refine the estimated value for 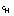 .
. - In informal discussion, the question arose about treatment of ocean heat flux in open water and mixed (ice concentration less than 1) model grid cells. In most models, including PIPS 2.0, ice will not form until surface heat extraction has cooled the upper ocean to freezing. It was pointed out that in the seasonal pack of the Weddell Sea, the mixed layer seldom if ever reaches its freezing temperature, hence would not grow ice under this restriction. Our recommendation is that (2) serve as an upper bound on heat extraction from the ocean, so that if outgoing (upward) energy flux in open water exceeds (2), ice would grow to conserve enthalpy. This would allow ice growth with mixed layer temperatures above freezing and would better describe seasonal ice regimes akin to the Weddell Sea. Since the upper bound implied by (2) increases with
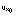 (proportional to wind speed) as well as
(proportional to wind speed) as well as 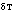 , in practice it is difficult to grow ice with mixed layer temperatures more than a few tenths of a degree above freezing.
, in practice it is difficult to grow ice with mixed layer temperatures more than a few tenths of a degree above freezing.- Ice/Ocean Salinity Flux
- Salinity flux at the ice/ocean interface depends on basal melting or freezing and freshwater input from surface or internal melting which percolates through the ice or runs off at floe edges. The latter may be expressed in terms of a vertical velocity of the interface as it adjust isostatically to surface or internal melting:
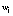 . The basal melt or freeze rate may be similarly expressed as a vertical interface velocity,
. The basal melt or freeze rate may be similarly expressed as a vertical interface velocity, 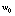 , which depends on the kinematic ocean heat flux (
, which depends on the kinematic ocean heat flux (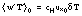 ) and heat flux conducted away from the interface in the ice cover:
) and heat flux conducted away from the interface in the ice cover: 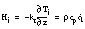 where kc is ice thermal conductivity. A good approximation of salinity flux is given by
where kc is ice thermal conductivity. A good approximation of salinity flux is given by 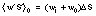 where
where 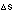 is the difference between mixed layer and ice salinities. The salinity flux boundary condition is thus
is the difference between mixed layer and ice salinities. The salinity flux boundary condition is thus
- where
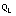 is latent heat of fusion (adjusted for brine volume) divided by
is latent heat of fusion (adjusted for brine volume) divided by 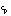 (McPhee, 1992). This formulation should be weighted by ice concentration, and modified to include a direct precipitation/evaporation flux condition over open water.
(McPhee, 1992). This formulation should be weighted by ice concentration, and modified to include a direct precipitation/evaporation flux condition over open water.- Restoring to Climatology
- Use the new Environmental Working Group (EWG, 1997) climatology rather than Levitus (Levitus and Boyer, 1994).
- Longer Term Goals
- There was strong consensus that good ice/ocean coupling requires either a high vertical resolution ocean model with good boundary layer parameterization, or a separate embedded mixed layer model. This is thought to be especially important near the ice margins (Zhang et al., 1998) and in regions of high variability associated with bottom topography.
- Model treatment of fluxes at the ice/ocean interface should be adjusted to the complexity and vertical resolution of the underlying ocean model, and should take into account increasing sophistication of the ice model (e.g., summer insolation through thin ice categories). Much work remains in characterizing undersurface roughness.
- Improvements in understanding and modeling turbulent exchange in the pycnocline was identified as an important facet of coupled models, especially for understanding heat exchange within the entire system.
- Ice response to tidal, inertial, and other relatively high frequency motions needs more attention than it has received, especially as model resolution improves. This is particularly important in shallow marginal seas and marginal ice zones.
- Modeling upper ocean fronts and eddies, and their impact on sea ice requires sufficient horizontal grid spacing to adequately resolve the internal deformation radius, of order 10 km in polar oceans.
- Buoys measuring mixed layer and other upper ocean characteristics in polar oceans should be utilized to the maximum extent possible for model verification and real time data assimilation.
- References
Environmental Working Group (EWG), NSIDC, Boulder, CO, Web Site: http://ns.noaa.gov/atlas, 1997.
Levitus, S., and T. Boyer, NOAA/NESDIS CDROM, 1994.
McPhee, M. G., J. Phys. Oceanogr., 9, 388-400, 1979.
McPhee, M. G., Sea Ice Processes and Models, R. Pritchard, ed., University of Washington Press, Seattle, 62-75, 1980.
McPhee, M. G., J. Geophys. Res., 97, 5365-5379, 1992.
McPhee, M. G., C. Kottmeier, J. H. Morison, in press: J. Phys. Oceanogr., 1998. Available in pdf electronic format-- contact miles@apl.washington.edu.
Zhang, J., W. Hibler, III, M. Steele, and D. Rothrock, J. Phys. Oceanogr., 28, 191-217, 1998.