INCLUDING THERMALLY-INDUCED STRESSES IN PIPS James K. Lewis Ocean Physics Research & Development, Long Beach, Mississippi 1.0 Introduction As pointed out recently by Overland and Weeks [1996], the overall strength of a region of pack ice in the Arctic is dependent upon a collection of features within that region. These features include refrozen leads, smaller-scale floes (~100 m), and larger floes (>1 km). The floes themselves may exhibit a range of strengths, with older, thicker (>0.5 m) floes being weakened by flaws generated by thermal fracturing. Thus thermal processes can directly impact the deformation of the pack ice in a region by modifying the strength of floes. Moreover, the horizontal transmission of stress within the ice pack may be modified by the background (thermally induced) stress state of individual floes, and certainly the thermal stress state can be modified by motion-induced stresses (which tend to be compressive in nature), which can alter the onset of thermal fracturing. Thus an understanding of the thermal stressing of floes is important in understanding the deformation of Arctic pack ice. A formulation has been developed for the consideration of thermally-induced stresses in pack ice. This formulation goes along with those ideas for the enhancement of handling internal thermodynamics by utilizing multiple layers in the vertical to predict heat flux within and through the ice-snow media. Such an approach with the thermodynamics has been coupled with a mechanics formulation for predicting thermally-induced stresses in floes. 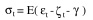2.0 Mechanics 2.1 Rheological Formulation The governing equation relating stress (positive being compression) and strain rates is where 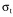is the time rate of change of stress, E' is the effective elastic modulus, 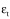is the thermally induced strain rate, 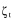is a mechanically-induced strain rate, and 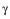is the strain rate as a result of the viscous creep of a material under stress. The parameterization used for E' was derived by Lewis [1993] based on observed variations of E' and T, STR, and P: E'(T,P,STR) = 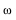log (STR + 3) + 3.5 GPa [(1 - 7.5472 P) (1 - 0.0714 T)] where STR = |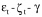| is the overall strain rate for a given time and depth in the ice, T is the ice temperature (degrees Celsius), and 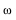= 0.1 GPa per log(STR). We use a modification of the Nixon and McRoberts [1976] two-term viscous formulation as modified by Richter-Menge and Cox [1995]: 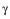= 1.86 x 10-15 (1 - T)-5.25 [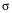/(1 - P1/2)2]n + 3.63 x 10-29 (1 - T)-2.09 [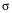/(1 - P1/2)2]4 where the units are s-1, 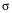is stress in pascals, P is the total porosity of the ice layer, T is the ice temperature (oC), and n has a value of 1.36 (1 - T)0.19. The 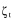term reflects strain transmitted throughout the ice as a result of the floe being too large to bend or twist in response to spatial variations of strain rates. 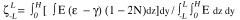For ice of thickness H, the mechanically induced strain rate in the x direction (relative to a fixed coordinate system on the floe) is given by where 2L is the extent of the horizontal variations of the snow cover thickness and N is the fractional coverage of any cracks (whether continuous or not) in the x direction at a depth z in the ice. The stress in the y direction is calculated as above except the integrals are with respect to z and x. In calculating an appropriate 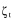term, the snow cover distribution information must be used. 2.2 Fracturing Paradigm Fracture toughness studies of ice concern the prying open of a crack. 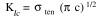The parameter worked with is the critical stress intensity factor KIc, which is related to the overall tensile failure stress of the ice by the relationship [Mellor, 1986] where c is the half-length of the crack. If a crack runs through the entire thickness of the ice, c would be half the horizontal length of the crack. For 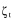< 10-3 s-1, which is typical for thermally induced strain rates, KIc is approximately constant, with experimentally determined values for this constant ranging from 35 to 125 kPa m1/2. Observations also indicate that KIc decreases with increasing temperature [Mellor, 1986]. This is likely a reflection of the fact that sten increases as the ice becomes colder. 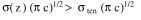At this time, the fracturing paradigm is such that if at depth z for some c, fracturing will be assumed to occur if N(z) is nonzero (meaning c is nonzero since N(z) = 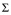c(z) divided by 2L). However, if we make the assumption that c is relatively constant within a floe, specifying c is not required, and the fracturing criteria reduces to 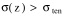. To use this criteria, we consider the work of Dykins [1970] who provided data on the variation of the uniaxial tensile strength of saline ice as a function of temperature T and salinity S: 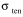= (-348.9 + 19.8 T + 17.9 S - 0.9 T S) kPa. Previous studies indicate that |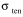| << |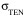|; that is, thermal fracturing is observed to occur at background stress levels within floes that are considerably less than the measures tensile strength of saline ice [Lewis, 1994; Lewis et al., 1994]. On the basis of the observed stress levels and the corresponding under-ice noise due to thermal fracturing from these previous studies, we use 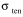= 0.05 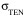. This allows for varying fracture toughness as the tensile strength of the ice changes. Now we must specify how much stress relief will occur as a result of any fracturing. Studies indicate that stress relief for fracturing that is approximately the scale of the ice being fractured results in a final stress that is ~45% less than the maximum stress [Mellor, 1986, p. 210]. However, one can expect that as the size of the ice specimen becomes larger with respect to the size of the flaw, the stress relief should become smaller. In terms of my parameter N, I expect that stress relief -> 45% of 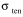as N -> 1.0 and stress relief -> 0.0 as N -> 0.0. We will assume a linear variation between these two extremes. Thus, when 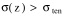, the model-calculated stress is reduced to 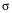(1 - N) + 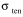0.55 (N). With this fracturing criteria and this expression for stress relief, we can simulate the thermally induced stresses of an ice layer at a given time for a given snow cover, given the vertically varying N(z). 3.0 Required Observations Studies have shown that the rheology and fracturing paradigm produce reasonable predictions of the observed stresses in both first-year and multiyear floes by estimating the vertical variations of existing cracks in the ice. One of the keys to the mechanics is the flaw structure parameter N(z) associated with thermally induced fracturing in pack ice.` We have no data pertaining to N(z) and lack formulations for "aging" nearly flaw-free first-year floes to flawed multi-year floes. At this time, we have to approximate the flaw structure based on matching observed stresses with predicted stresses . The best means of estimating N(z) is through the collection of stress data at several sites on floes. Moreover, such sampling requires several observations of stress in the vertical. On the basis of observations of thermally active flaws in first-year ice [Lewis et al., 1994], actually sampling flaw structure poses a practical problem in that the sizes of such flaws are apparently of the order of at least 5-10 m. Sampling at smaller scales would likely underpredict the true flaw structure of a floe. One possible means of determining flaw structure is by the use of acoustic tomography [Subramaniam et al., 1993] since the propagation of acoustic waves in ice will be modified at flaw boundaries. Another factor deals with the porosity of the ice. Porosity effects the effective elastic modulus as well as the creep of the ice. There exists no data on the systematic variations of gas volumes in sea ice. This leaves only porosities determined from cores whenever they are taken, but these may changes considerably during the spring when there is melt water percolating down through the ice. Sensitivity studies need to be performed as to the impact on stress predictions of utilizing specified porosity profiles based on data bases and idealized floe characteristics. References Dykins, J. E., Ice engineering-tensile properties of sea ice grown in a confined system, Tech. Rep. R689, U.S. Navy Civ. Eng. Lab., 1970. Langley, A. J., 1989: Acoustic emission from the arctic ice sheet. J. Acoust. Soc. Am., 85 (2), 692-701. Lewis, J. K., A model for thermally-induced stresses in multiyear sea ice, Cold Reg. Sci. Technol., 21, 337-348, 1993. Lewis, J. K., Relating Arctic ambient noise to thermally-induced fracturing of the ice pack, J. Acoust. Soc. Am., 95, 1378-1385, 1994. Lewis, J. K., W. B. Tucker III, and P. J. Stein, Observations and modeling of thermally-induced stresses in first year sea ice, J. Geophys. Res., 99(C8), 16361-16371, 1994. Mellor, M., Mechanical behavior of sea ice, in The Geophysics of Sea Ice, edited by N. Untersteiner, pp. 165-281, Plenum, New York, 1986. Nixon, J. F., and E. C. McRoberts, A design approach for pile foundations in permafrost, Can. Geotech. J., 13, 40-57, 1976. Overland, J. E., and W. F. Weeks, Studying Arctic sea ice at two scales provides more accurate picture, Eos Trans AGU, 77, 501-506, 1996. Richter-Menge, J. A., and G. F. N. Cox, Creep of saline ice at low stresses and high temperatures, paper presented at 5th Int. Offshore and Polar Engineering Conference, The Hague, Netherlands, June 11-16, Vol. II, 312-316, 1995. Subramaniam, D. R., G. V. Frisk, J. A. Doutt, and C. J. Sellers, Determination of compressional wave and shear wave speed profiles in sea ice by crosshole tomography - Theory and experiment, J. Acoust. Soc. Am., 93, 721-738, 1993. Stein, P. J., 1993: Predictions and measurements of the directivity of a monopole source in a floating ice plate. In Natural Physical Sources of Underwater Sound (B. R. Kerman, ed.). Kluwer Press. 625-639.