James K. Lewis, Ocean Physics Research & Development
207 S. Seashore Avenue, Long Beach, MS 39560
ocnphys@aol.com, 228-865-0059
There are several components in the U.S. Navy's Polar Ice Prediction System (PIPS) that deal with the thermodynamics of the ice and snow cover. These include ice edge melting, melt pond formation, ice growth, and heat flux through the snow and ice. Here we focus on the issue of the flux of heat through the snow and ice, with some consideration of ice growth and melting at the ice-water interface. The treatment of these "interior" thermodynamics is of great importance in producing reliable predictions of ice thickness characteristics and the flux of heat and salt across the ice-water interface. Recently, Blitz et al. (1996) showed that modifying just the vertical resolution of the temperature profile in a model of heat flux through ice can alter the time scale of interannual ice thickness variability by more than a factor of 2. Moreover, Lewis (1998) has shown that some of the thermodynamic parameters for sea ice can be up to an order of magnitude different for newly-grown (first-year) ice and older (multi-year) ice. These types of findings point to the need to provide accurate representations of the interior heat fluxes in PIPS.
2. THERMODYNAMICS IN THE EXISTING PIPS 2.0 MODEL
The existing formulation for handling the heat flux through the snow and ice in PIPS 2.0 is based on the work by Parkinson and Washington (1979) and Manabe et al. (1979). This formulation balances the surface heat flux by the conduction of heat through the ice beginning at the ice/water interface. This is done in a vertically-averaged manner. The thermal conductivity is calculated in PIPS 2.0 as a weighted sum of the snow thermal conductivity Ks (0.31 W/m/oK) and the ice thermal conductivity KI (a constant of 2.1656 W/m/oK).
Overall, the formulation used in PIPS 2.0 is appropriate for simulations with longer time steps (of up to a month) in that, under those circumstances, the thermal inertia of the ice is a small component of the heat balance. Basically, the existing PIPS heat flux formulation neglects that fact that it requires 1000 cal to change the temperature of 1 kg of ice by 1oC.
At this point, PIPS 2.0 is running with a time step of 2 hours. The impact of thermal inertia can be considered at such time scales using analytical solutions to the vertical heat flux governing equation (Lewis and Denner, 1988). Diurnal surface heat flux variations result in a thermal wave penetration depth of ~20 cm. Thus, the great majority of the heat flux variability triggered by the diurnal surface forcing occurs within the top 20-30 cm of the ice. The lower parts of the ice do not sense the diurnal surface heat flux variability. As the frequency f becomes smaller and approaches that of 1 cycle per 5 days, the analytical solution of Lewis and Denner shows that the ice temperatures at various depths fluctuate in near unison, with the vertical gradient being close to linear.
Thus, there will be certain situations in which the heat balance used by PIPS 2.0 will not be appropriate for a model which is resolving surface heat variations on the order of hours. This contention is supported by under-ice ambient noise data. Acoustic data from springtime indicate significant temperature variations in the upper levels of pack ice that occur with the development of strong daily shortwave heating and nightly cooling (Lewis and Denner, 1987). Moreover, such short-term heat flux variations also have been identified during the fall based on under-ice noise data (Lewis, 1994).
The formulation in PIPS 2.0 for the growth or melting of ice at the ice/water interface employs a constant freezing point for sea water as well as a constant volumetric heat of fusion for ice. PIPS 2.0 is coupled with a dynamic ocean model that provides estimates of the salinity and temperature of the oceanic mixed layer directly under the ice. However, this water temperature and salinity information is not utilized is estimating the freezing temperature of the sea water. But more importantly, the salinity of the water is not employed in determining a salinity of the ice as it freezes or the value of the latent heat of fusion.
In the existing PIPS 2.0 heat flux formulation, a salinity for the ice is not considered. However, expressions exist that relate the growth of ice to the salinity of the under-lying ocean mixed layer. Cox and Weeks (1988) developed a thermodynamic model for the growth of first-year ice, and that model included salinity uptake in the freezing process. A formulation was used that considers the salinity of the ice as well as the rate of freezing (the greater the freezing rate, the higher the salinity of the new ice). Moreover, expressions exist which can be utilized to determine the change of salinity profiles in sea ice as it ages (Cox and Weeks, 1975, 1986). The importance of knowing salinity is in the fact that 1) the thermal conductivity, 2) the specific heat, and 3) the latent heat of fusion of ice are all functions of salinity and temperature. Moreover, as the ice melts it is actually releasing into the oceanic mixed layer water that may be up to 3-7o/oo in salinity as opposed to 0o/oo.
There are a number of ways in which the interior thermodynamics of PIPS 2.0 could be enhanced. These range from keeping the existing expression (1) but with thermal inertia to utilizing a complete thermodynamic model with multiple levels in the snow and ice. All the more recent studies show that the use of multiple levels in the snow and ice provides a much more accurate estimate of heat flux. But care must be taken to develop enhancements that are physically accurate but computationally practical.
One suggestion is the utilization of multiple levels in the snow and ice using a variable vertical coordinate system. In such a situation, the physics being modeled is the vertical flux of heat within an ice or snow layer of thickness H,
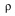 c (
c ( 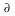 T/
T/ 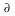 t) = (k
t) = (k 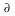 T/
T/ 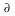 z)U - (k
z)U - (k 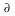 T/
T/ 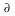 z)L (1)
z)L (1)
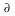 T/
T/ 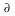 z)U and (k
z)U and (k 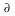 T/
T/ 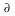 z)L are the
conductive fluxes of heat at the top and bottom of the layer, respectively. The model divides the floe into horizontal
layers, the thicknesses of which would vary with time as the snow cover or ice thickness changes.
z)L are the
conductive fluxes of heat at the top and bottom of the layer, respectively. The model divides the floe into horizontal
layers, the thicknesses of which would vary with time as the snow cover or ice thickness changes.Sigma-Coordinates
A time varying vertical grid structure has been used in the modeling of the atmosphere and ocean for a number of years. This type of system is referred to as sigma-coordinates, and models with such coordinates typically allow user-specified vertical spacing. At the very least, an ice/snow thermodynamic model would have 3 levels of snow cover (if any) and 3 levels of ice. This allows for the user to specify a thin level near the air interface with which to specify surface fluxes, 2 thin levels on each side of any snow-ice interface to better specify fluxes between 2 media with different thermal conductivities, a thin level at the bottom of the ice with which to specify bottom fluxes, and 2 middle levels (one in the ice, another in the snow) for representing the average temperatures within the ice and snow. As the total thickness changes with each time step, the thicknesses and temperatures of each of the levels would be adjusted slightly, just as in other sigma-coordinate models.
Implicit Solution Technique
With the application of the appropriate expression at the surface layer, (1) at subsurface layers, and an under-ice water temperature, it can be shown that the vertical flux of heat can be formulated in N equations in N unknowns, where N is the number of layers in the snow and ice. These N equations are in the form of a tridiagonal matrix, and can be solve quite efficiently using implicit techniques. Thus, an enhancement of the PIPS 2.0 interior thermodynamics to that with vertical resolution can utilize relatively large times steps in solving for temperature structure. The methodology could be expanded to included flux calculations for each thickness category within a grid cell.
Parameter Values - The Impact of Salinity
To utilize (1), the values of specific heat and thermal conductivity must be specified. Also, for ice growth and melting, we must specify a value for the latent heat of fusion for ice. All these parameters are functions of temperature and, in the case of ice, salinity. The thermal conductivity of ice varies from 2.0 to 2.5 W/m/oK, and the latent heat of fusion of ice is only weakly dependent on salinity and temperature. However, the specific heat of ice can vary from ~2000 to 21000 J/kg/oK depending on temperature and salinity. Thus, including ice salinity in the model provides better estimates of the true heat flux for both thin ice (typically more saline) and thicker ice (typically more fresh). Since PIPS 2.0 is being run in conjunction with an ocean model with a mixed layer, it would be logical to utilize the salinities as well as temperatures in the growth module of PIPS to determine the freezing temperature as well as the amount of salt uptake as the ice freezes.
Cox and Weeks (1988) provide expressions for the growth of first-year ice including the uptake of salt under freezing conditions. Using these expressions allows the ice within the model to take on a characteristic salinity, and this will impact the determination of the specific heat of the ice. However, we know that, as the ice "ages", the salinity changes through brine expulsion and gravity drainage. Means of specifying these effects have been determined through experiments (Cox and Weeks, 1975, 1986). As such, these aging effects can also be included in the thermodynamics (Lewis, 1998). The impacts of these effects is greatest on first-year ice salinities, and it has been found that are in a degree "self-limiting" in that they do little to modify the salinities of multi-year ice.
5. REFERENCES
Bitz, C. M., D. S. Battisti, R. E. Moritz, and J. A. Beesley, 1996: Low-frequency variability in the Arctic atmosphere, sea ice, and upper-ocean climate system. J. Climate, 9, 394-408.
Cox, G. F. N., and W. F. Weeks, 1975: Brine drainage and initial salt entrainment in sodium chloride ice. Tech. Rpt. 82-30, U.S. Army Corps. Eng. Cold Reg. Res. Eng. Lab., Hanover, NH. 85 pp.
Cox, G. F. N., and W. F. Weeks, 1986: Changes in the salinity and porosity of sea ice samples. J Glaciol., 32, 371-375.
Cox, G. F. N., and W. F. Weeks, 1988: Profile properties of undeformed first-year sea ice. CRREL Rep. 88-13, 57 pp.
Lewis, J. K., 1994: Relating Arctic ambient noise to thermally induced fracturing of the ice pack. J. Acoust. Soc. Amer., 95, 1378-1385.
Lewis, J. K., 1998: The thermo-mechanics of pack ice. In press, J. Geophys. Res.
Lewis, J. K., and W. W. Denner, 1987: Arctic ambient noise in the Beaufort Sea: seasonal space and time scales. J. Acoust. Soc. Amer., 82, 988-997.
Lewis, J. K., and W. W. Denner, 1988: Higher frequency ambient noise in the Arctic Ocean. J. Acoust. Soc.
Amer., 84, 1444-1455.