Lab 4 Background Information

Computing the Energy Density Spectrum

We will use the Matlab function fft(x) to do the Fourier Analysis of the data. This is the discrete Fourier transform of vector x, computed with a fast Fourier transform algorithm (FFT). If X is a matrix, fft(x) is the FFT of each column of the matrix. (In Matlab, all variables are matrices; vectors are simply row or column matrices.)

The fft function employs a radix-2 Fourier transform if the length of the sequence is a power of two, and a slower mixed-radix algorithm if it is not.

The inverse fast Fourier transform of vector x is ifft(x).

The two functions implement the transform – inverse transform pair given by

where N=length(x). Note that the series is written in an unorthodox way, running over n+1 and k+1 instead of the usual n and k because Matlab vectors run from 1 to N instead of from 0 to N-1.

To make the connection between familiar formulas from the notes and those listed above, recall that the transform pair as we usually see it looks like this:

where 2p/T = w₁ = fundamental frequency, and

The Matlab equations at the top only differ from the discrete form of our usual pair by a factor of 1/N. To show this, we can define

and rewrite the equation for X(k+1) as

If we then strategically multiply and divide by delta t, we have

Recall that in discrete notation, dt becomes delta t, with T = N*(delta t), and t becomes k*(delta t). With these relationships, it should be clear that this modified equation for A(k+1) is a discrete version of the above continuous equation for F(k). After substituting for X(k+1), the equation for x(n+1) becomes

Careful placement of delta t results in

This equation now parallels the above equation for g(t), where here t becomes n*(delta t) and again T = N*(delta t). You will note, however, that Matlab computes its sum with only positive indices (0 to N-1 instead of –N/2 to N/2). This will not affect your final computation of the energy density spectrum below; you will just need to be careful when you “fold over” the amplitudes to compute G_x.

If x is a vector of size N, then Ax = fft(x) is a complex vector of size N. If you plot Ax versus frequency, you will see that these amplitudes are symmetrical about N_f rather than zero. We want to estimate the energy density spectrum using the following:

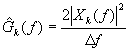
so that for NS samples

You will use a coded version of the above two equations in your lab 4 program for your computations of Gx and Gxmean, respectively.