
 |
Geodesy for the Layman - Table of Contents |
Trigonometric functions, sines and cosines, are harmonic in that they repeat themselves after a certain interval. Harmonic Expressions, formed by combining sines, cosines and arbitrary constants, are mathematical devices for curve-fitting and interpolation in either two or three dimensions. An example of a harmonic Expression for a two-dimensional curve is
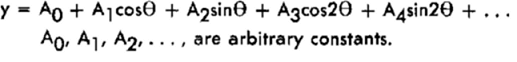
where A(sub0), A(sub1), A(sub2),..., are arbitrary constants.
The nature of every harmonic expression is that the constant term (AO in the equation above) equals the mean or average value of all points on the curve. The succeeding terms represent harmonic deviations from that mean value. Each harmonic term has two parts: the trigonometric part which is harmonic and controls the frequency of the oscillations, and a constant multiplier which controls the amplitude. For the second term in equation (1)
cos(theta) is the trigonometric part and A(sub1) is the constant multiplier.
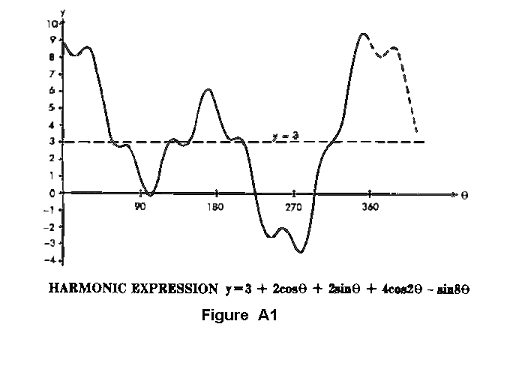
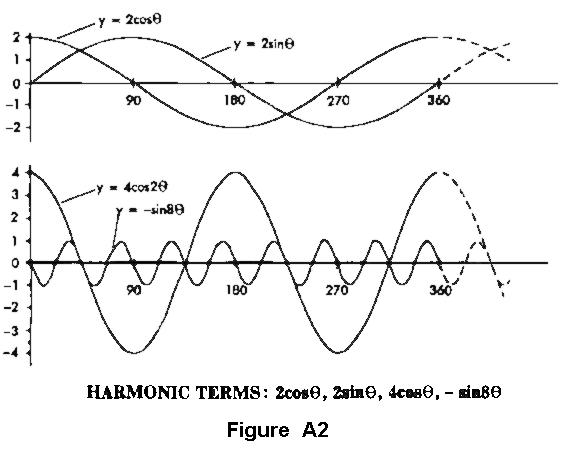
which describes the curve shown in Figure A-1. Its first term, which is its constant term, is 3.
Thus 3 is the mean value of the curve. The second term, y = 2cos(Theta), y = 2sin(Theta), y = 2cos(Theta) y = 4cos2(Theta) y = -1sin8(Theta),
1. Legendre Functions
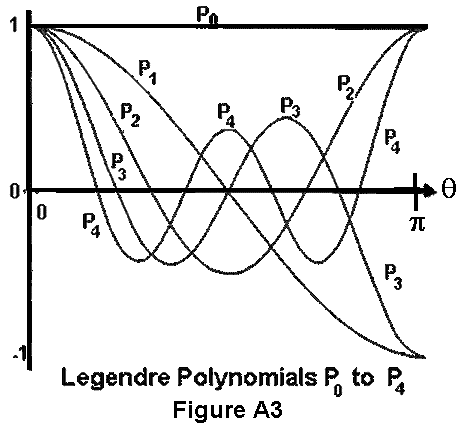
The basic spherical harmonic form is the Legendre polynomial, Pn(cOso), given by the
Formula
where n, a nonnegative integer, is the degree of the polynomial. The Legendre polynomials for
degrees n = 0 through n = 5 are:
Graphs of these polynomials up to n = 4 are shown in Figure A-3.
Another form of spherical harmonics are the associated Legendre functions, P(subnm)(cos(Theta)),
where m, a nonnegative integer smaller than or equal to n, is the order of the function. When
m = 0, this function becomes P(subn0)(cos(Theta)), or simply the Legendre polynomial P(subn)(cos(Theta)).
The surface spherical harmonics are Legendre functions multiplied by cos m(Lambda) or sin m(Lambda),
where (Lambda) is the longitude,
and so on.
These resultants are tesseral harmonics, which divide the sphere into blocks of alternate
positive and negative values, called tesserals. Figure A-4 shows a typical tesseral harmonic. The
shaded areas represent tesserae where the harmonic is positive, and the non-shaded areas repre-
sent negative tesserae.
A special case arises when m = 0, in which case the sin m(Lambda) harmonic terms disappear
because sin O(Lambda) = 0. When m = 0, the tesseral harmonic divides the sphere into zones of alternate
positive and negative values, and is therefore called a zonal harmonic. An additional special case
arises when m = n. Then the tesseral harmonic divides the sphere into sectors of alternate positive
and negative values. Hence they are called sectorial harmonics. Examples of zonal and sectorial
harmonics are shown in Figure A-4.
2. Surface Spherical Harmonics
The general expression for the surface spherical harmonic of an arbitrary function f((Theta),(Lambda)) is
where A(subnm) and B(subnm) are arbitrary constants. For simplicity and easier handling, the harmonics
in Equation (3), commonly referred to as conventional harmonics, can be replaced by other func-
tions called fully normalized harmonics. The surface spherical harmonic then becomes
where the bar indicates that the harmonic term is fully normalized. The conventional and fully
normalized terms are related through the following expressions
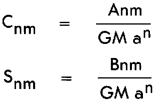
In many applications, geopotential coefficients, symbolized by C and S, are used in harmonic
expressions rather than the A and B coefficients. Like the A and B coefficients, they can be used in
either conventional or fully normalized form. The relationship between the two types of coeffi-
cients is.
where a is the equatorial radius and GM is the gravitational constant. Fully normalized geo-
potential coefficients, C and S, can be obtained from the conventional coefficients, C-BAR and S-BAR,
by means of an expression similar to Equation (5).
The expression for the earth's gravitational potential, that is, the potential of the attraction
of the earth, is
where
The ability to express the gravitational potential by Equation (8) lies in determining proper
values for the harmonic coefficients, C-BAR and S-BAR. These coefficients are a function of the mass
distribution of the earth, which unfortunately is not known. Thus, the coefficients have to be
computed in some other way, such as, from artificial satellite perturbations or gravity obser-
vations on the surface of the earth.
In the expression for the gravitational potential, the constant term, U = GM/r, which is the
n = 0 term, equals the mean value. The mean value of the earth's gravitational potential
is the value which would occur if the earth were a sphere. As in the two-dimensional case, each
term after the mean value represents a harmonic deviation from that mean value. As was pre-
viously stated, the magnitude of the coefficients, C-BAR and S-BAR, is related to the mass distribution
of the earth. Thus, where the potential is positive with respect to the mean value, there is a
mass excess. Similarly, there is a mass deficiency where the potential is negative.
The following discussion will analyze in detail some of the lower degree harmonic terms.
In order to simplify writing, conventional harmonics will be used in this portion of the discussion.
Equation (8), expressed in terms of conventional harmonics, is
If this equation is expanded, the harmonic terms for degrees 1 and 2 are:
1. Degree n = 1
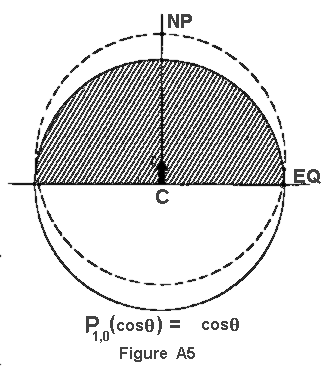
Figure A-5 shows a geometric representation of the harmonic term P(sub10)(cos(Theta)). The solid
circle represents the mean value and the dashed curve is the value of the potential when only
the mean value term and the term under consideration are combined. Thus, the dashed curve
shows the effect of an individual term. The hachured part of the figure indicates the area of the
sphere where the harmonic is positive; and the non-hachured part indicates where the harmonic
is negative.
is positive in the northern hemisphere and negative in the southern. As is shown in Figure A-5,
this corresponds to there being a mass excess in the northern hemisphere and a mass deficiency
in the southern hemisphere. If this were true of the earth, the center of mass would be north
of the center of coordinates. Since it is always specified that the center of coordinates and the
center of mass coincide, this harmonic is not admissible in the potential expression and therefore
must equal zero. In order to make this term zero, the coefficient C(sub10) is set equal to zero, so
that the entire term disappears.
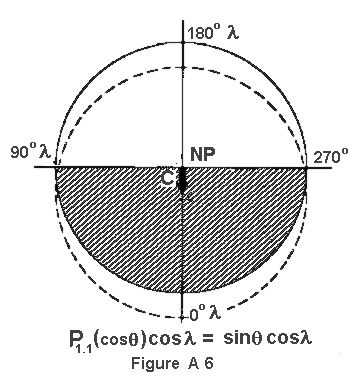
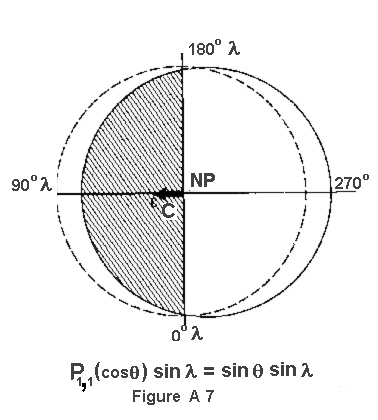
The P(sub11) (cos(Theta)) terms are shown in Figures A-6 and A-7. They represent hemispheres
(eastern and western) of positive and negative values. Existence of the terms indicate a shift of the
center of mass away from the center of the coordinates in the positive hemisphere. Each term repre-
sents different hemispheres of positive and negative values, shifted by 90(Degree), since cosx and sinx
are 90(Degree) out of phase. The same logic which applied to the harmonic P(sub10)(cos(Theta)) applies here
and these harmonics are also inadmissible. Thus, their coefficients, C(sub11) and S(sub11), are set equal
to zero, so that the terms disappear.
2. Degree n = 2
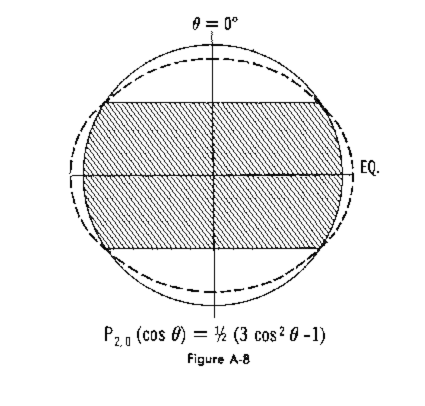
The zonal harmonic P(sub20)(cos(Theta))is shown in Figure A-8. In the figure, the constant C(sub20) is
assumed to be negative, thus representing a mass excess in the equatorial region and a mass
deficiency in the polar regions. Such a mass distribution indicates that the earth must be flattened
somewhat. Actually, the magnitude of the C(sub20) coefficient is 10(sup2) times greater than that of any of
the other coefficients. This indicates the extent to which the earth is flattened and the importance
of this harmonic.
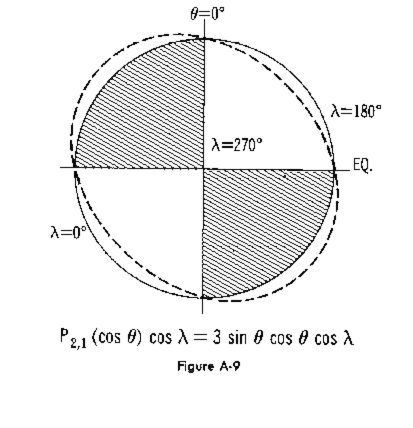
The next harmonic term in order is the P(sub21)(cos(Theta))cos(Lambda) term shown in Figure A-9. As
indicated by the figure, it represents opposite northern and southern quadrants of mass excesses
and deficiencies. This would make the axis of inertia revolve around the axis of rotation of the
earth, thus causing the earth to wobble on its axis. Since there is really some wobbling, which
is commonly referred to as precession, the coefficient C(sub21) cannot equal zero. However, the pre-
cession is so small the C(sub21) is also very small. In many cases it is approximated by zero and
the term disappears. There is also a sin(Lambda) term which has similar geometry, except that the quad-
rants are shifted by 90(Degree) in longitude. The same logic applies.
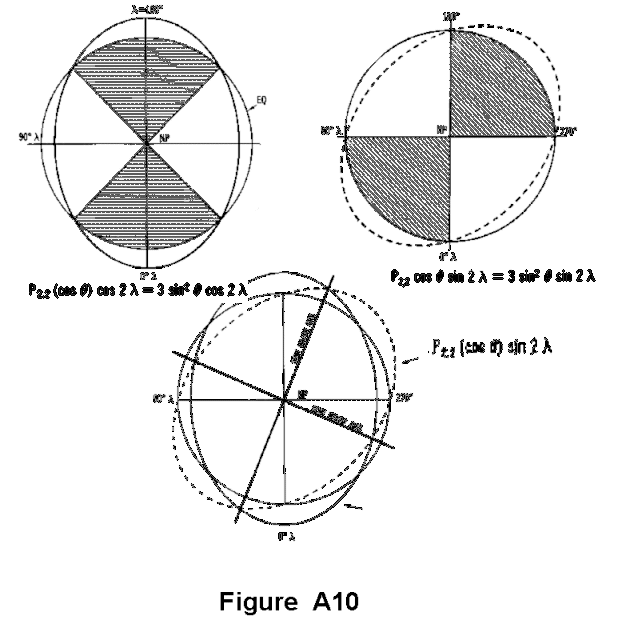
The next two terms are the sectorial harmonics P(sub22)(cos(Theta))cos2(Lambda) and P(sub22)(cos(Theta))sin2(Lambda),
shown in Figure A-10. The figure shows sector quadrants which would indicate ellipticity of the
equator. Each term represents ellipticity in a different direction. Thus, the two terms must be
combined to obtain the overall ellipticity of the equator. The direction of the semimajor axis of the
equatorial ellipse is at the point where their sum is a maximum. The direction of the semiminor
axis is 90(Degree) from the semimajor axis. As shown in Figure A-10, the sum is a maximum where the
two curves meet. This is only true if their coefficients, C(sub22) and S(sub22), are equal. The value for the
ellipticity of the equator can be determined from the values of the coefficients C(sub22) and S(sub22).
3. Degrees n = 3 and n = 4
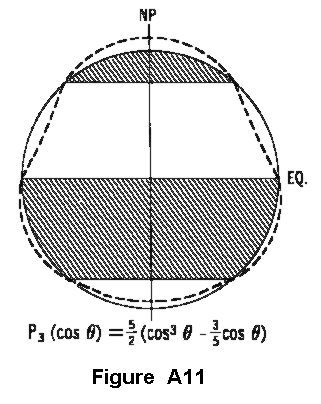
The presence of the zonal harmonic P(sub30)(cos(Theta)) indicates that the earth is pear-shaped,
as shown in Figure A-1 1. For this reason, this term has been referred to as the pear-shaped
harmonic. Since values have been computed for its coefficient C(sub30), the earth is considered to be
somewhat pear-shaped.
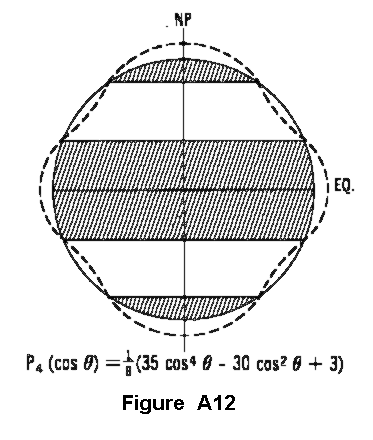
The last harmonic term that will be mentioned here is the zonal harmonic P(sub40)(cos(Theta)),
shown in Figure A-12. Although it has no recognizable geometric relationship, it is important
because it is a term of the normal gravity Formula and permits refinement of the potential on
an ellipsoid.
There are an unlimited number of functions which can be expressed in terms of spherical
harmonics. One of these functions is the normal gravitational potential of the reference ellipsoid.
The normal gravitational potential V, which is the gravity potential of the reference
ellipsoid minus the potential of centrifugal force, can be developed into a series of zonal spherical
harmonics
where
For this application, the J coefficients are usually used rather than the C coefficients. There is a
constant relationship between the different coefficients.
In some applications involving the reference ellipsoid, equation (9) is truncated at n 2,
giving
Mathematical expressions for the J2 and J4 coefficients are
where
Equation(10) shows the relationship between the flattening and the J2 coefficient. An
example of ageodetic application of artificial earth satellites is to determine J2 from satellite
perturbations,and to use that value in equation (10) to determine the flattening.
END OF DOCUMENT
Figures Cleaned Up 9-9-2002 Naval Postgraduate School
![]()
B. SPHERICAL HARMONICS
In the geosciences, a commonly used form of harmonics are the surface spherical harmonics.
These functions are much used in geodesy because they are relatively simple to use and because
the earth's shape can be approximated by a sphere. The coordinates normally associated with
spherical harmonics are the spherical coordinates: radius r, co-latitude or polar distance (Theta), and
longitude (Lambda).
![]()
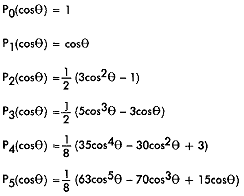
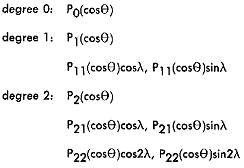
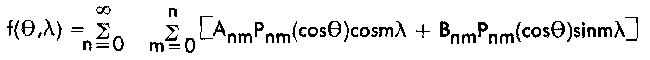
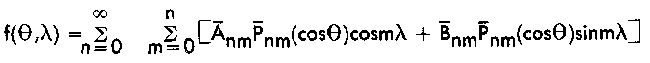

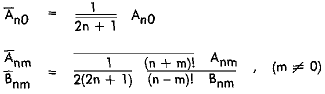
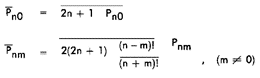
C. GRAVITATIONAL POTENTIAL OF THE EARTH
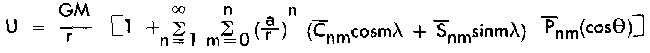

D. ANALYSIS OF LOWER DEGREE HARMONIC TERMS
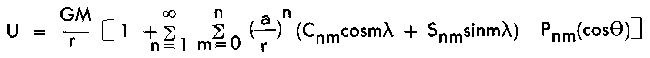
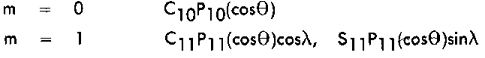
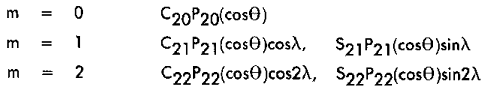
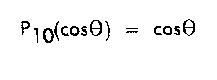
E. APPLICATIONS OF SPHERICAL HARMONICS
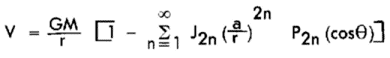

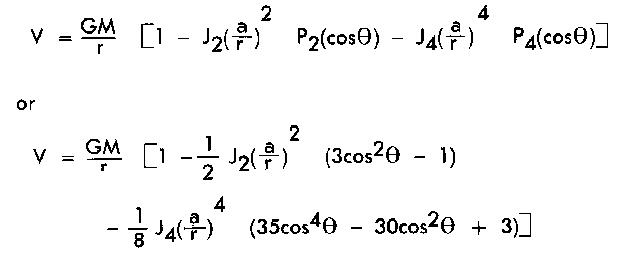
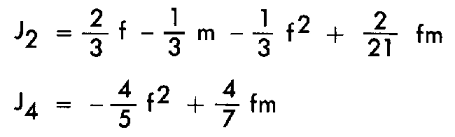

Point of Contact: GOG
Phone Numbers:
Com. (314)263-4071
DSN 693-4071
Email: gandg@nima.mil
NIMA HTML Last Updated 1 February 2002