The Shape of the Earth
  
previous next

Rotating Bodies and Forces

 

If a rigid body rotates there is an outward force on all parts of the solid. This is also true for rotating fluids.  This can be easily experienced using an old fashion toy that consists of a small ball on a string that is rotated in a circle.

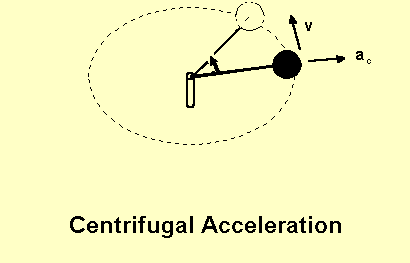
Centrifugal Acceleration Toy

 

Holding the toy by the handle you will feel the force as the ball rotates. The faster it rotates, the more the force. Also if you increase the length of string keeping the period the same, the force increases.

The force is also proportional to the mass of the ball. Double the mass and you double the force. Newton's second law tells us that where there is a force, there is acceleration. The force is given by
 
 
 

F = ma

 
  Where m is the mass, a is the acceleration and F is the force. If a force is proportional to the mass, as it is in this case, then it makes sense to talk about the force per unit mass, or the acceleration. This is the result of the force the hand feels. The acceleration of the mass is called the centrifugal acceleration.

This acceleration is directed outward from the center of the rotation. It is given by the product of the "moment arm" (radius in the picture) and the square of the rotation rate - in natural units.

 
 

 
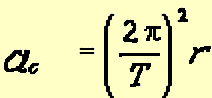
  Here T is the period of the rotation - the time to make one revolution, and the Greek letter pi is the value 3.14159.....

For the earth the first term is constant. The earth rotates once a day, so roughly the value in brackets is

2 * 3.1416 / ( 24 hours * 60 minutes/hour * 60 seconds/minute)

or .000,072,9 radians/sec ( 7.29E-5 in computer notation). [Note, this value uses the true rotation period of the earth. This is about 4 minutes faster than a 24 hours.]

 
Previous
 Top
      Next