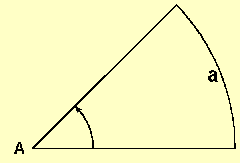
Draw a part of a circle, called an arc of a circle. Call the angle between the two radii A and the arc of the circle "a".

Now construct two identical sectors adajacent to each other. Clearly the total angle is 2A and the total arc lenght will be 2a.

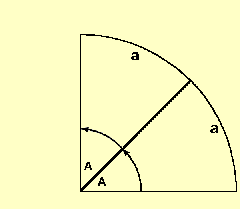
Thus the arc lenght is proportional to the angle. Let the distance along the arc be the angle times the radius times some constant, K,

a = K rA

K will be a function of the units chosen for the angle. Notice that both the radius r, and the arc length "a" have length units.

The special choice of K = 1 produces what are called the natural units for an angle. These are called radians. This means that the angle in radians is just the ratio of the arc length divided by the radius.

Here the arc length and raduis must be in the same units ( meters,or kilometers, or miles for example).

To find out exactly what a radian is, examine a complete circle. Now the arc length is the circumference of the circle.  We know the arc length from the equation for the circumference:

so that

In degrees we know that A is 360 degrees. Therefore

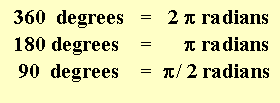
The value of pi is about 3.14, or more precisely 3.14159 or even more precisely 3.14159263578793 ... The value of pi has no exact reprenstation in the decimal system. This is like 1/3. But unlike 1/3, pi does not repeat itself. It also has no exact representation in any number system. It is called an irrational number. It is not the ration of any two integers, no matter how big the numberator and demoninator.

Because the value of pi is known, at least approximately, we can find what the value of 1 deg or 1 radian is in the other units.

1 deg = 0.0017453... radians

= 1.7453.. mrad

Where a mrad is one thousandth of a radian.

1 rad = 57.296... deg.

Here the abreviation for radians, rad, is used.

It is interesting to note that the  angular unit of a second of arc ( 1/(60*60)  of a degree)  is about  5 microradians,

 1"  =   4.848...  urad

Here the notation of a double quote to denote arc seconds is used as is the abreviation of urad for microradians.  A microradian is one millionth of a radian.

If you have ever used a program language like BASIC, C, or Fortran, you have found that the trigometric functions take an argument in radians. A lot of scientic hand calculators also compute the sine (sin) and cosine (cos) funtions. Many take either radians or degrees. Some take only radians.