

Now that you've decided on a three-dimensional model, and can choose the domain size that is appropriate for the problem at hand, the next set of choices you need to make have to do with the resolution in space and time.
The fundamental problem is that the equations that govern the motion of the atmosphere and ocean are continuous. In order to solve them on a computer, we need to discretize the domain, that is, create a grid system of points on which to solve the equations.
The schematic below shows a typical model grid system.
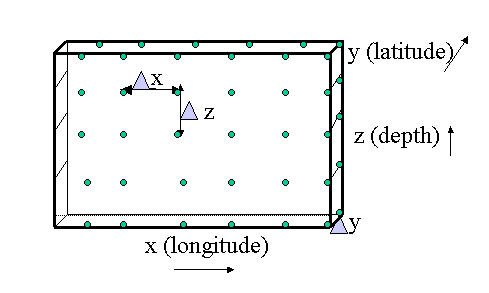
The variables of interest, the temperature, salinity, and velocity components,
are solved at the grid points, denoted by green dots in the schematic. The distance
between two grid points at which say temperature is solved is denoted by
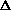 x.
Likewise, the distance between two grid points in the y direction (usually latitude),
is denoted by
x.
Likewise, the distance between two grid points in the y direction (usually latitude),
is denoted by 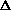 y.
The distance between two depth or pressure grid points in the vertical,
is denoted by
y.
The distance between two depth or pressure grid points in the vertical,
is denoted by 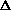 z.
The distance between grid points can be variable. For example,
finer vertical resolution is normally required near the ocean surface, and
finer horizontal resolution near coasts, where the variability is
greater.
Therefore, many models have smaller grid spacing in the vertical
near the surface than say below the thermocline (region of greatest temperature change).
Note that
z.
The distance between grid points can be variable. For example,
finer vertical resolution is normally required near the ocean surface, and
finer horizontal resolution near coasts, where the variability is
greater.
Therefore, many models have smaller grid spacing in the vertical
near the surface than say below the thermocline (region of greatest temperature change).
Note that 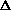 z is always less than
z is always less than 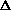 x
and
x
and 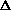 y; there is no requirement for
y; there is no requirement for
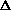 x to equal
x to equal 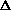 y,
although often it does.
Later, we will discuss several different ways the vertical grid can be represented.
y,
although often it does.
Later, we will discuss several different ways the vertical grid can be represented.
How do you choose the resolution, that is, the 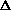 x,
x,
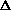 y, and
y, and 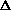 z values for a model? There are competing aspects to consider when deciding how fine
a resolution to choose, that is, what the grid spacing and time step of the model should be.
z values for a model? There are competing aspects to consider when deciding how fine
a resolution to choose, that is, what the grid spacing and time step of the model should be.
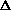 t must be less than
the horizontal grid spacing,
t must be less than
the horizontal grid spacing, 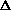 x.
In other words, the wave (or advective process) must not move farther
than 1 grid point per time step.
This can be written mathematically as:
x.
In other words, the wave (or advective process) must not move farther
than 1 grid point per time step.
This can be written mathematically as:
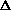 t <
t < 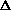 x.
x.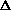 t,
which is
t,
which is
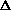 t <
t < 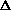 x / c.
x / c.The activity you are about to do will illustrate the trade-offs among these three aspects.
Your job is to set the time step, 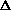 t, and the grid spacing,
t, and the grid spacing,
 x, such that
the problem is computationally stable, and the velocity is optimally resolved
in time and space, without wasting computer time.
x, such that
the problem is computationally stable, and the velocity is optimally resolved
in time and space, without wasting computer time.
 When you're ready, do the
online activity.
When you're ready, do the
online activity.
As the previous activity demonstrated, much smaller time steps are needed for a given spatial resolution, when the advective, or wave, speed c is greater. In the ocean, 200 m/s is a typical speed for surface (also called external, or barotropic) gravity waves, while 2 m/s is more typical for internal, or baroclinic, gravity waves. Instead of solving the full set of primitive equations at the small time step needed for fast surface gravity waves, a method called mode-splitting, is commonly used to improve computational efficiency. Only the barotropic, or shallow water equations (discussed earlier), which are simpler than the full primitive equations, are solved using the short time step, while the more complicated equations for the baroclinic modes are solved using a slower time step.
There are other more subtle implications of the choice of model resolution involving computational truncation and round-off errors, but we will not go into those here.
Be aware that you cannot determine the temporal and spatial resolution of a model solely by looking at the graphical, or other, output. Often, the model results are subsampled in time and/or space for output, and occasionally they are interpolated (so the output has finer resolution than the model grid or time step).
Next, we'll look at various horizontal and vertical grid types.