

The number of dimensions in a model tells us the number of directions along which variables change in the model. In a curvilinear coordinate system, there are 3 orthogonal (meaning perpendicular, or at right angles to each other) directions, plus time. If fields are allowed to vary in all 3 directions, then the variations in any arbitrary direction can be derived. If fields are also allowed to vary in time, then we can predict the value of any variable at any location at any time. This is what is meant by the 4D Cube.
If the coordinate system is rectilinear (i.e. follows straight lines), as well as orthogonal, then it is called a Cartesian or rectangular coordinate system.
See http://mathworld.wolfram.com/CoordinateSystem.html for more information on coordinate systems.
The three spatial dimensions are often longitude (E-W), latitude (N-S), and depth (or height); denoted as x, y and z, respectively. The components of velocity along these directions are usually denoted u, v, and w. Usually a right-handed coordinate system is used where x is positive towards the east, y is positive towards the north and z is positive upwards; but sometimes in the ocean z is taken to be positive downward and a left-handed coordinate system is used.
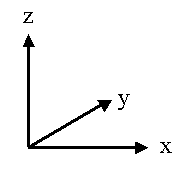 | 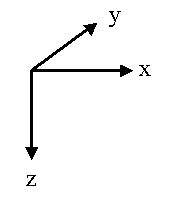 |
| Right-handed coordinate system | Left-handed coordinate system |
Another common choice for regional coastal models is the cross-shelf and along-shelf directions and depth. In this case, you have to be especially careful that you know what direction, and with what sign, the variables are defined. For instance, positive y (v) may be alongshelf and towards the north, positive x (u) cross-shelf and towards the coast, and z (w) positive upward, but other choices are possible.
Another kind of curvilinear coordinate system that is often used in global ocean models is the spherical coordinate system.
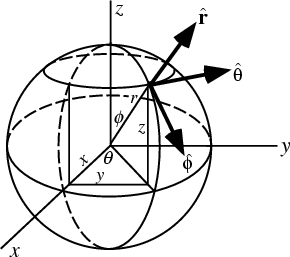
Generally, when we describe a numerical model as being one, two or three-dimensional, we are listing the number of spatial dimensions. The fourth dimension, time, is unspoken.
For one-dimensional models, which dimension do you think is most commonly used?
Hint: Think about the scales of motion discussed in the previous module on oceanography.
Remember, 1D models assume everything is uniform, or homogeneous, in the other two dimensions, while a 2D model assumes everything is uniform in the third dimension. 1D, 2D, and 3D models are used for both research and operational purposes. NAVSAR in GFMPL includes a 1D surface layer model; the Navy's tide prediction models, ADCIRC and PCTides, are run as 2D models, and the circulation models, SWAFS and POM, are 3D.
Answer the following questions before proceeding to the next box:
If you were to design a model of the ocean circulation for the Pacific Ocean, how many dimensions would you use?
Now you're ready to continue to the next step in the process of designing a model - click on the box labeled "Model Physics" in your browser window.