By taking the laws of physics and treating the ocean as a body acted on by forces, mathematical equations are obtained whose solutions can be used to help understand the movement of ocean waters. Numerical ocean modeling solves approximate forms of these equations using computers. In this section we examine the physics of the major type of ocean model used in forecasting and nowcasting: the primitive equation model. Models using simplified physics are also discussed. As well, methods are discussed to account for processes that are too small to be resolved by the model grid, but nevertheless are important.
Consider Newton's Second Law of Motion (F = ma). This relationship says that if a force, F, acts on a body with mass, m, the body will acquire an acceleration or rate of change of velocity, a. In other words, if something pushes on a body it will speed up or slow down. Note that bold face type represents a vector, which has both a size, or magnitude, and direction). Let's start with some one-dimensional examples.
When an object is dropped, or falls off the table, it accelerates as it falls because of the force of gravity (F = mg). A block is placed at rest on a horizontal table and we apply a small force to it. It does not move. This is because of the opposite frictional force exerted by the table on the block, acting along the surface of contact. As the applied force is increased, it overcomes the frictional force and the block starts to move and then accelerate.
In the ocean, we can describe the force balances on a parcel of water as
The mathematical form of these equations in vector form is:
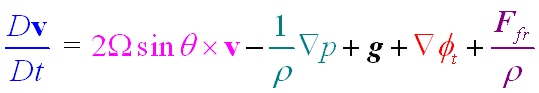
In the equation above, v is the vector velocity, which consists of the components u, the velocity in the x-direction, v, the velocity in the y-direction, and w, the velocity in the z-direction.
These equations are known as the Navier-Stokes equations, where the fluid is assumed to be incompressible. Remember that the assumption of incompressibility means that these equations, and the models based on them, can not be used to model how sound travels through the ocean.
Terms in the Navier-Stokes Equations:
| Acceleration term: |
|
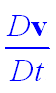
This term is composed of the local rate of change due to time variation, plus the rate of change due to advection of the flow. Ultimately, one of the most important things we want to get out of the model is how the currents change with time. That's what this term tells us. This is the a in a = F/m. Everything on the other side of the equation are the forces that cause this acceleration. |
| Coriolis term: |  |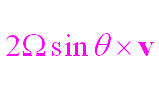
As was explained earlier, the Coriolis force is not a real force, hence it was not listed above in the statement
of forces.
It appears because we normally make measurements and predictions relative to axes fixed to earth,
which is itself rotating about its axis.
The symbol 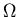 represents how fast the earth is spinning in space.
The angular speed of rotation on any point on the earth also depends on latitude,
 .
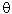The symbol f, also known as the inertial frequency, is often used to represent the Coriolis force.
|
| Pressure term: |
 |
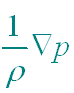Just as in the atmosphere, the pressure in the ocean varies from place to place and those differences
are expressed as a gradient, represented by the symbol  .
These pressure gradients, which can be thought of as a parcel of water being pushed harder from
one side than the other cause movement to occur.
The two contributing factors to pressure gradients are sea level slopes
(this is the barotropic component introduced earlier) and changes in density
(this is the baroclinic component discussed earlier).
|
| Gravity | g | The force acting toward the center of the earth. |
| Gravitational tidal potential |  |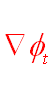
This term accounts for the ocean tides resulting from variation in the gravitational pull from the sun and the moon, as has been described in more detail earlier in this course. |
| Frictional forces: |  |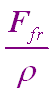
At the ocean surface, this term includes the force of the wind, or windstress,
denoted by the symbol  . Similarly, there is a
bottom stress, which is discussed in more detail below.
|
Even with advanced computers, these equations are too complex to solve explicitly for large domains over long periods of time, so further simplifications are made:
Boussinesq Approximation:
Density variations are small in the ocean (less than 3%) so density,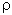 
,
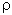is replaced by o (~1035 kg m-3)
except in terms involving the gravitational acceleration g.
Hence the approximation is made in the horizontal, but not the vertical, momentum equations.
Effectively this says that since density variations are small, their effect on the
mass
of the fluid can be neglected, but not their effect on the weight (mass times gravity)
of the fluid parcel.
Hydrostatic Approximation As noted earlier, the hydrostatic approximation is valid when vertical accelerations are small relative to the gravitational acceleration. Given that the ocean width is so much greater than its depth, this is generally a valid approximation.
Using these two approximations, a mathematical description of the ocean circulation can be given by a coupled set of seven equations. These are known as the primitive equations.
Numerical ocean models based on these equations are known as Primitive Equation Models. Examples:
Advantages of primitive equation models:
Disadvantages of primitive equation models:
These disadvantages have led to the use of models with simpler physics models. These are discussed in the next two sections.
As discussed in the Approximations secton, the geostrophic approximation is a first order balance (terms that are larger than others usually by a factor of 10 or more) between the Coriolis force and the pressure gradient force. It assumes that the flow is steady (no acceleration) and inviscid (no friction).
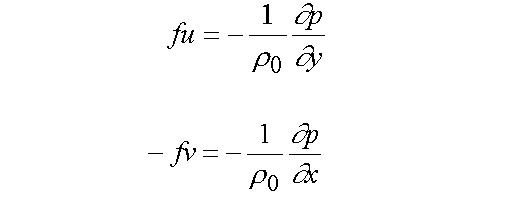
Geostrophic currents can be computed from these equations using the pressure gradient obtained by integrating the hydrostatic equation,
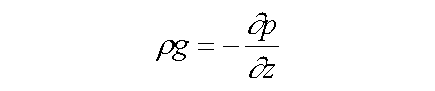, which in turn uses density calculated from measurements of temperature and salinity. This is known as the dynamic method and represents the simplest ocean model. The currents from MODAS are geostrophic currents.
A shallow water model is used to examine barotropic processes that disturb the ocean surface. Examples are barotropic tides, inverted barometer effects and wind setup or seiching.
Assumptions:
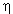.Due to the hydrostatic approximation and constant density, the horizontal pressure gradients are
independent of depth and therefore represent the change in sea surface height .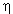
The velocities are therefore also independent of depth and represent depth-averaged flow.
In its unforced, inviscid (frictionless) form,
the shallow water model is
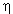in the horizontal directionA forced shallow-water model includes a term representing the surface stress and bottom stress due to friction.
The 2D versions of ADCIRC and PCTides run by the Navy are based on the shallow water equations.
A fluid, like the atmosphere or the ocean, is continuous in space. If the equations governing the motions of the fluid were very simple, we could come up with solutions that are continuous in space. However, because the equations are very complex, we have to estimate the continuous solutions by solving a discretized set of equations using computer programs. By discretized, we mean that we solve for values of all the variables (velocity, temperature etc.) on a discrete set of grid points, rather than along a continuum like a line (more on this later).
. . . . . . . . . . . . rather than ______________________
In numerical models, we need a way to represent the processes that are so small that they are happening between the grid points; yet they affect the larger scale processes that are directly modeled. These methods are called subgridscale closure schemes. They are also called turbulence closure schemes. If we were to introduce fluctuating, or turbulent, velocity components to the set of variables being solved for, 3 new variables would be added and 3 extra equations (in addition to the 7 outlined above) would have to be solved for. The term "closure" comes from the fact that these schemes allow us to account for the turbulent velocity components in terms of the existing seven variables, so no extra equations are needed. In other words, in order to have a "closed" system of equations, described above, we have to parameterize the processes that are not resolved by the chosen grid. These subgridscale processes include:
Why is it so important that we parameterize and account for these small-scale processes on the larger-scale system? Some of the reasons are that:
There are two major types of subgridscale mixing processes: lateral (horizontal) mixing, which prevents the pileup of energy in the wavelength corresponding to the mesh (grid) size and vertical mixing, which includes the surface mixed layer, convection, and the bottom boundary layer.
Different turbulence closure schemes may produce significantly different model results. The formulation of these schemes is quite complex, and they are introduced in only a very rudimentary fashion below.
Parameterizations for lateral mixing:
Lateral mixing is often parameterized in terms of an eddy diffusivity and properties of the larger scale flow that are resolved. Specifically, the variations in space of the spatial gradients of velocity are related to the turbulence.
Parameterizations for vertical mixing:
Parameterizations for bottom friction:
The bottom friction is usually parameterized in terms of the interior velocity (i.e. the flow above the bottom boundary layer). In the simplest parameterization, the bottom friction is represented as an empirically derived drag coefficient times the magnitude of the interior velocity. This is known as linear friction. More commonly, the bottom friction is parameterized as the product of a drag coefficient times the square of the interior velocity, called quadratic friction. Bottom friction parameterizations may vary across the model domain as a function of depth, and in more sophisticated schemes take into account the bottom sediment grain size which can affect the bottom roughness, and hence the bottom friction. There are also parameterization schemes that predict how the bottom friction will vary as a function of the surface wave field. These effects can be particularly important in shallow water.
The range of spatial and temporal scales of motions in the ocean is seen in the following figure. It extends from seconds to centuries in time and from meters to thousands of kilometers in space. This presents a challenge for numerical models and is one of the reasons why models are not "one size fits all". Very short time steps (order seconds) are needed to simulate the "fast" processes, but very long model runs (order decades) are needed to simulate the "slow" processes. It would take tremendous computer resources to run models with very short time steps for very long times. Therefore, people have come up with clever ways to handle this for different situations.
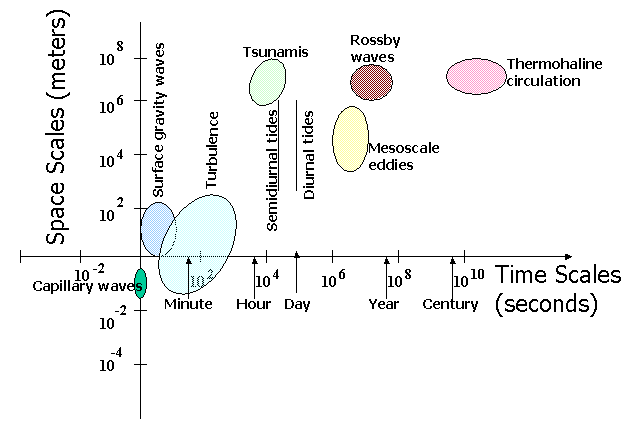
The ocean's response to surface forcing can largely be divided into two types: fast barotropic response via surface gravity waves and relatively slower baroclinic adjustment via other types of waves. Long surface gravity waves have speeds of order (gH)1/2 where g represents gravity and H is the ocean depth; a typical speed is 200 ms-1. These wind-driven and tidal waves and surges can be up to several meters high at the surface. The large-scale baroclinic response has much longer time scales and smaller surface elevation variations. Even extreme events, such as those associated with El Niño and La Niña in the Pacific Ocean, have surface elevation changes (as measured by the TOPEX/POSEIDON altimeter) of only a few tens of centimeters.
Since the time step restriction for surface gravity waves is much more stringent (often by a factor approaching 100) than for other processes, one approach has been to replace the free surface with a "rigid lid", which eliminates surface gravity waves in the model. This is done by specifying that there be no vertical motion at the model surface, i.e. w = 0 @ z = 0, where w is vertical velocity and z is the vertical coordinate. This approximation causes only a very small change to the long baroclinic waves (also called Rossby or planetary waves). The approximation does not imply that the free surface displacement corresponding to the baroclinic modes is negligible. It only implies that the vertical displacements at the surface are much smaller than those within the fluid column, hence the numerical constraints are valid. Nor does it imply that the pressure is constant at the surface; if there truly was a rigid lid at z = 0, then the pressure on the lid would vary due to the baroclinic motions.
The usefulness of this approximation was demonstrated in an early ocean modeling effort. An Ocean General Circulation Model (OGCM) developed by Bryan (1969), Cox (1970; 1984), and Semtner (1974) was developed for climate studies where it would be run for times of order thousands of years. Removing the surface gravity waves allowed them to use time steps of several hours or longer for the very coarse resolutions possible with computers three decades ago.
The barotropic flow, however, must still be calculated as it has been modified, not eliminated. As model resolution increases and bathymetry becomes more complex, the advantage gained by the rigid lid approximation is lost by this computationally intensive calculation. As well, this calculation is difficult to carry out efficiently on modern computer architectures. As a result, free-surface models are now used extensively. A mode-splitting technique, to be discussed later, is used to avoid the time step limitation imposed by the fast gravity waves. For storm surge and tidal modeling free surface dynamics must be retained.
You're ready to go to the next step in the process and choose a domain for your model.